By Junqi
In data processing systems, pagination (Top-K) queries are a common and important operation used to extract the most representative or highest-priority K records from large datasets. Specifically, a Top-K query sorts a data source (for example, a table) by a chosen criterion, such as a numeric value, timestamp, or relevance score, and returns the top K records. Common use cases include:
• Leaderboards (for example, ranking by score or sales)
• Recommendation systems (for example, returning the top K relevant items)
• Real-time queries (for example, the latest K news items or most recent K transactions)
Data for these queries is read from data sources (typically table files), processed through multiple stages (such as filtering, joins, and projection), and finally reduced to the top or bottom K values.
When the data source consists of many files, traditional Top-K approaches usually scan and filter every file completely and then perform time-consuming computations, causing heavy I/O and CPU overhead. This inefficiency is especially pronounced for pagination query scenarios where users page through different segments of the Top-K results.
Existing solutions often process files serially in a single thread, lacking parallel processing and therefore forming Top-K thresholds slowly. They also typically lack a dynamic threshold update mechanism, so they cannot quickly exclude records that will not appear in the final Top-K, which further increases I/O and compute work. PolarDB for Xscale (PolarDB-X) overcomes these limitations by using multi-threaded cooperation, dynamic threshold updates, and optimized file scan policies. These techniques enable early termination of reads and computation, substantially improving pagination efficiency for complex queries.
In SQL, Top-K queries are typically expressed using the ORDER BY and LIMIT keywords. Any query can append the following clause to the end of the statement to perform a Top-K query:
ORDER BY col1 ASC|DESC, col2 ASC|DESC, ...
LIMIT offset, lenThis query sorts the result set by the specified columns (col1, col2, …, colx) in ascending (ASC) or descending (DESC) order, and then returns len rows starting from the offset position.
For example, the SQL statement below filters tables R, S, and T, joins them, and then paginates the final result ordered by R.col1 ASC and R.col2 DESC.
select * from R inner join S on S.A = R.A inner join T on T.B = R.B
where R.condition_1 and S.condition_2 and T.condition_3
order by R.col1 asc , R.col2 desc limit offset, len;Below is the implementation of a classical Top-K algorithm suitable for single-threaded, small-scale scenarios.
A min-heap is a binary heap where each node's value is less than or equal to its child nodes' values. The top of the heap (root node) always contains the smallest element in the heap.
A simple Top-K algorithm using a heap can be implemented in the following way:
1. Initialize a min-heap H of size K.
2. Scan the dataset A and insert each element A[i] into the heap until H contains K elements. At this point, the top of the heap H[0] is the smallest among them.
3. Continue scanning the remaining elements in the dataset, compare them with the top element of the heap and perform replacement if needed:
• If the current element is greater than the heap's top element, pop the top element from the heap and insert the current element. The heap will then automatically adjust itself to maintain the heap property.
• Otherwise, skip the current element and proceed to the next.
4. After the scan completes, the K elements in the min-heap are the dataset's Top-K largest elements.
The core principle behind the algorithm, and specifically Step 3 ("comparison and replacement"), is:
During the finding of the Top-K elements of a set, for any subset of size ≥ K, an element that is smaller than that subset's Kth largest element cannot belong to the final Top-K set.
In the simple Top-K algorithm above, the heap H contains K elements:
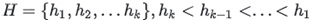
The Kth largest element in H is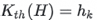 
For each element A_i in the dataset A, form a new set by combining A_i with the current heap elements:
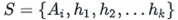
If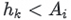 
, considering 
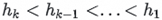as we discussed earlier, there exists a new size-K set H' whose Kth largest element is larger than h_k: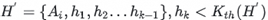 
Therefore, h_k can be safely discarded because it cannot be in the final Top-K.
When a database executes an SQL statement containing a Top-K clause, such as: ORDER BY col1 ASC|DESC, col2 ASC|DESC,... LIMIT offset, len, the most straightforward approach is:
1. Solve the Top-K problem with K = offset + len by constructing a min-heap of size K.
2. Build a comparator for all comparison operations including the heap sort: If the query specifies ascending order (ASC), the comparator must use reverse ordering. If the query specifies descending order (DESC), the comparator can use normal ordering.
Pseudocode of the comparator:
comparator(a, b) =
(s1 * cmp(a.col1, b.col1) != 0) ? s1 * cmp(a.col1, b.col1) :
(s2 * cmp(a.col2, b.col2) != 0) ? s2 * cmp(a.col2, b.col2) :
...
(sN * cmp(a.colN, b.colN))Where:
• cmp(x, y) is the basic comparison function (returns -1 if x < y, 1 if x > y, and 0 if x == y).
• si = -1 when the i-th column is sorted in ASC order.
• si = 1 when the i-th column is sorted in DESC order.
All subsequent comparisons are performed using this comparator.
3. After obtaining the Top-K results through the min-heap-based algorithm, the final SQL output is produced by selecting len rows starting from the offset-th record in the sorted Top-K set.
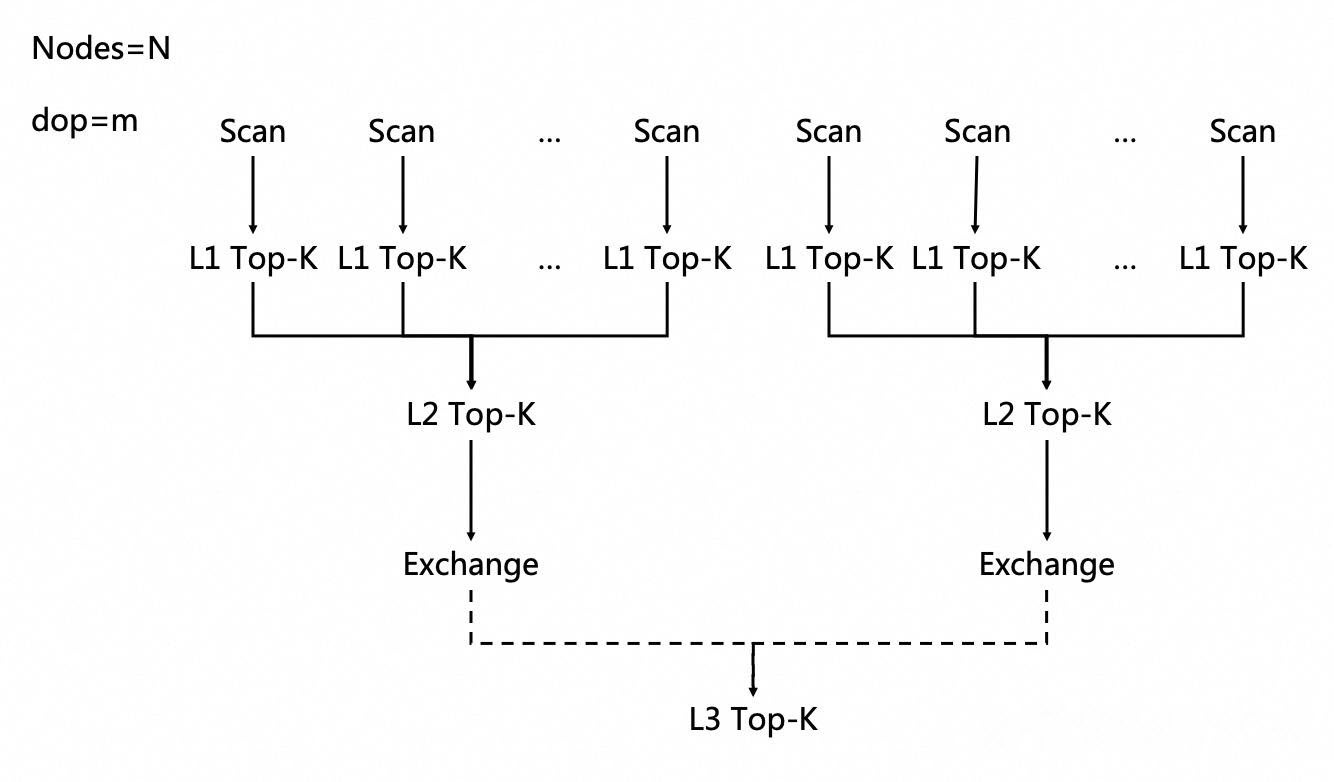
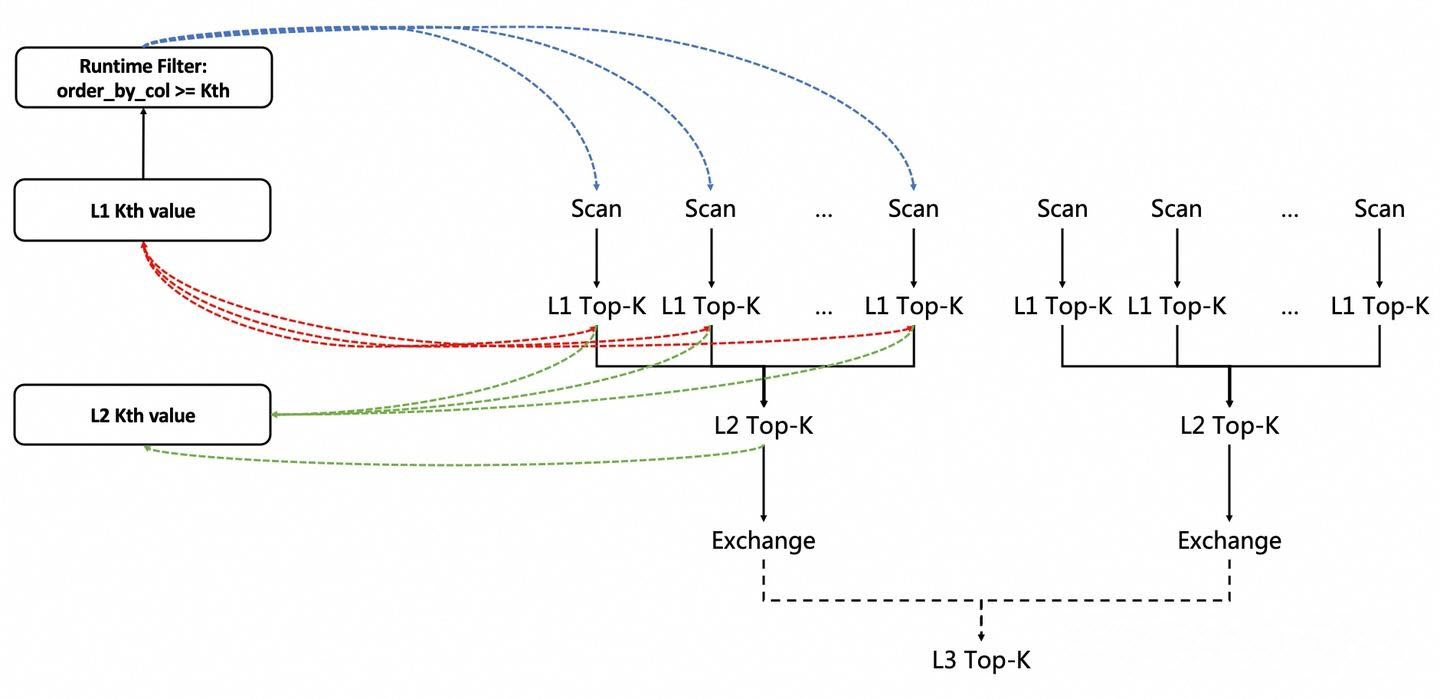
PolarDB-X introduces a parallel Top-K processing solution using a three-level Top-K operator structure: L1, L2, and L3. Each level handles Top-K aggregation and optimization at a different stage, reducing computational complexity compared with simple heap-merging methods. Multiple threads collaboratively update the global Kth largest value, accelerating threshold convergence and improving data filtering efficiency. Tight coordination between upstream and downstream operators further enhances query processing. The internal execution flow of each Top-K operator has also been redesigned to include heap-top cleanup and dynamic filtering steps.
In the computer cluster of a PolarDB distributed database, there are N compute nodes, with one master node acting as the query initiator and coordinator, while also performing worker tasks. The remaining nodes are worker nodes.
When a user initiates a Top-K query, the database instance builds a directed acyclic graph (DAG) for execution, based on the total number of compute nodes N and total parallelism m. Assuming parallel operators are evenly distributed across the nodes, the execution proceeds in the following way:
At all three levels (L1, L2, and L3), each Top-K operator maintains an internal min-heap of size K.
The diagram below illustrates the parallel scheduling workflow: Scan operators on each node feed data to L1 Top-K operators; L1 results are aggregated to the node-level L2 Top-K operator; L2 results are transferred through the Exchange operator to the master node's L3 Top-K operator, achieving fully parallel Top-K computation.
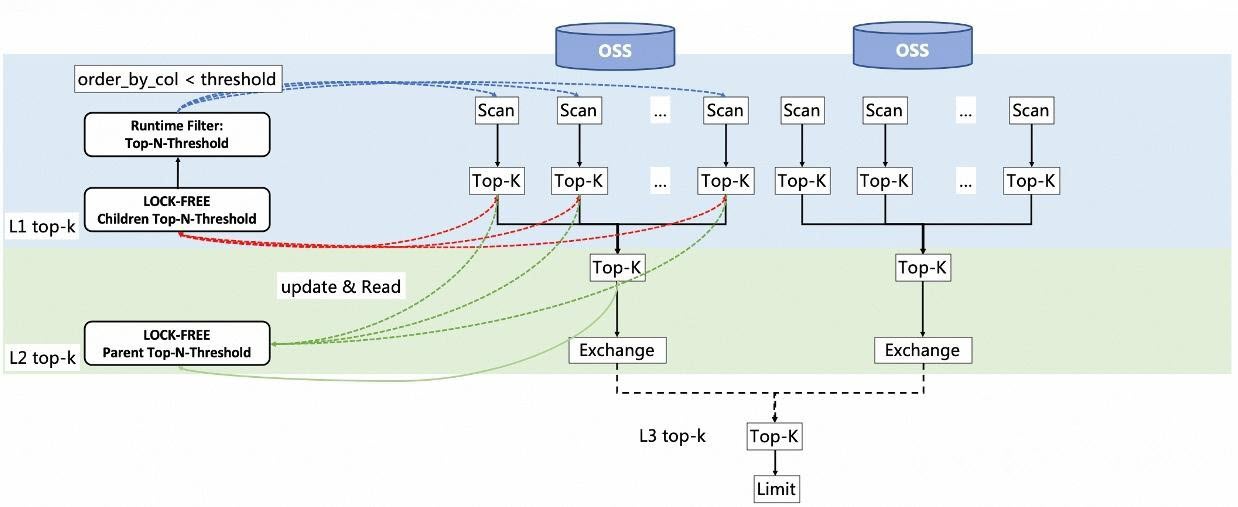
• Rationale for designing L1, L2, and L3 Top-K operators
• Performance advantages over single-core Top-K processing
.
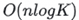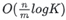
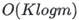
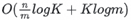
The speedup of multi-core Top-K compared to single-core Top-K can be approximated as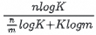 
In our scenario, both n (the total number of elements) and m (the number of cores or threads) are sufficiently large compared to K, so the speedup can be approximated as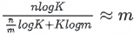 
This section describes how L1 Top-K operators collaborate both within a node and across nodes to accelerate the convergence toward the true global Kth largest value, reduce heap insertions, and improve the efficiency of Top-K computation.
All parallel operators jointly maintain a shared variable Kth, which represents the currently known global Kth largest value. This value could be a single-column value (val_col) or a vector composed of multiple columns ({val_col1, val_col2, ..., val_colx}). Through the collaboration of different parallel operators, the value of Kth gradually converges toward the true global Kth largest value Kth'. The faster Kth approaches Kth', the higher the data filtering rate, the fewer heap insertions are required, and the better the overall performance.
1. Initial state: At the time of L1 Top-K operator initialization, the total number of global elements is zero, so the Kth largest value (Kth) cannot yet be determined.
2. Element count updates: Within each node, every time a row is written into an L1 Top-K operator, the total number of elements written across all L1 Top-K operators on that node is updated. This update is atomic, thread-safe, and concurrent.
3. Initialization of Kth value: Once the global total number of elements reaches K, each L1 Top-K operator maintains a min-heap of size K. Then, the heap top elements are collected from all local heaps, and the smallest among them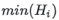 
is selected as the current global Kth. This completes the initialization of the Kth value.
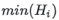represent the heap top (minimum value) of the i-th thread.
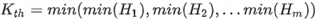, which corresponds to the Kth largest value in the overall Top-K candidate set.4. Concurrent Kth updates within a node: After the Kth value is initialized, all parallel operators concurrently and safely update the global Kth. Whenever a value is written into a Top-K operator, the operator compares and potentially updates the global Kth, aiming to raise its value and complete convergence as quickly as possible. This facilitates filtering, reducing unnecessary heap insertions and improving performance. The process works in the following way:
The underlying principle behind this step is that heap insertion takes O(logK) time, whereas comparing with the Kth value takes only O(1). Therefore, maximizing the use of the global Kth for early filtering can significantly reduce costly heap operations. While comparing with the local heap's root (top element) can also reduce insertions, the global Kth tends to be greater than any single thread's local heap root, and it is updated more frequently, thus converging faster. The relationship between a new value a and the global Kth can be summarized as:
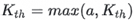
To ensure thread safety during updates to Kth, the following pseudocode shows the update logic per thread, using a Compare-And-Swap (CAS) mechanism to guarantee atomicity:
Function update_Kth_value(a):
Loop forever:
needUpdate = cmp(a, Kth_value) > 0
If not needUpdate OR cas_compare_and_set_Kth_value(Kth_value, a):
Break from loop
End Loop5. Cross-node Kth value update: After the Kth values are initialized and continuously updated within each node, each node periodically (usually every few tens of milliseconds) broadcasts its current Kth_i value to other nodes. Each node then computes the global Kth largest value and updates its local Kth accordingly: (N = Total number of nodes).
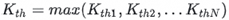
This step further accelerates the convergence of the global Kth value across the entire compute cluster.
This section describes the collaborative workflow between the L1 Top-K, L2 Top-K, L3 Top-K, and Scan operators.
In the parallel scheduling section, the basic execution flow of the DAG is described in detail. In addition to inputting upstream data and outputting data to downstream operators, there are additional collaborative relationships between upstream and downstream operators. The design of these relationships is one of the key focuses of this approach and plays a critical role in improving the overall Top-K query processing performance.
1. Runtime-filter for filtering data in the Scan operator: The PolarDB distributed database query engine supports the runtime-filter mechanism, which is a dynamic expression built by upstream operators and passed to the Scan operator as a predicate condition to filter scanned data. In this approach, if the user's Top-K query uses the format "ORDER BY col1, col2, ..., colx LIMIT offset, len", in conjunction with the Kth value maintained by the L1 Top-K operator, a predicate condition can be formed as (col1, col2, ..., colx) >= Kth, where Kth is dynamically updated and corresponds to a vector of values across x columns: Kth = {val_col1, val_col2, ..., val_colx}. The process works in the following way:
2. L2 and L3 Top-K operators utilize the order of upstream chunk outputs: Within the L2 Top-K and L3 Top-K operators, the upstream operators are L1 Top-K and L2 Top-K, respectively. Their outputs are ordered sequences of {Chunk_ij}, where Chunk represents the basic data unit in the database executor, typically containing 1,024 rows of data. Here, i represents the thread or operator from which the chunk originates, and j represents the index of the chunk within the i-th thread or operator. Although there is no inherent order between Chunk_ij from different threads, within each Chunk_ij, the rows are ordered in descending order based on the sorting columns. Therefore, when L2 and L3 Top-K operators encounter a row in Chunk_ij that is smaller than the current Kth value, all subsequent rows in that chunk will also be smaller than the Kth value and can be discarded directly, improving processing efficiency.
3. L2 Top-K's Kth_parent for filtering upstream L1 Top-K operators: In the L2 Top-K operator, the current Kth largest value Kth_parent is monotonically increasing and visible to the L1 Top-K operator. The L1 Top-K operator can check the value of Kth_parent to help filter input elements, and the principle is the same as the Kth value filtering. Since the input element sequences for L1 Top-K and L2 Top-K may not be in the same order, the convergence speed of Kth_parent and Kth may differ. Therefore, there is a probability that Kth_parent converges faster and reaches a higher value, resulting in better filtering performance.
The diagram below illustrates the collaboration between parallel operators and the upstream-downstream operators during the parallel Top-K query processing execution:
1. Red line: represents the shared and updated Kth value by the L1 Top-K operator, which is also used to filter data for the Scan operator.
2. Blue line: represents the Scan operator using a runtime filter {col >= Kth} to filter data, with the Kth value being updated and maintained by the L1 Top-K operator as part of the predicate condition.
3. Green line: represents the L2 Top-K operator maintaining the Kth value, which is used by the L1 Top-K operator for additional filtering.
L1, L2, and L3 Top-K operators share a unified execution logic, with internal flags distinguishing their levels.
1. Heap top cleanup: Before processing the chunk, each Top-K operator begins by cleaning its min-heap:
2. Kth-based row filtering: Check each row in the input chunk:
3. Data write to the min-heap: If a row passes Kth filtering, wrap it as a heap element a.
4. Kth value update: If the element a was successfully inserted into the heap and the heap size is now ≥ K, retrieve the heap top and update the Kth object with it. For more information, see the "Collaboration among L1 Top-K Operators – Concurrent Kth updates within a node" section.
5. Total element count update: Count how many elements were successfully inserted into the heap, and update the global total element count. Once this count reaches or slightly exceeds K, the Kth value is initialized. At the moment of initialization, the previous step cannot yet update Kth because the heap size is still ≤ K within each operator, and thus not yet eligible for Kth update. For more information, see the "Collaboration among L1 Top-K Operators – Initialization of Kth value" section.
For each level of Top-K operator (L1/L2/L3), once all input data has been fully processed, the operator enters a completed state. At this point, the total number of elements in the heap is less than or equal to K, as the processes of heap top cleanup, comparison, and filtering using the Kth value help identify and discard elements that cannot be part of the final Top-K result. The operator then repeatedly pops elements from the heap to form a descending sorted result sequence using the comparator. Let S_sorted = {a1, a2, ..., an}, where n ≤ K, represent the sorted result. This sequence is split into chunks and passed downstream, in the following way:
The specific implementation of PolarDB-X's parallel Top-K optimization has been introduced in the previous section. Now, for complex queries involving multi-table joins and pagination, where the row count of tables R, T, and S is in the billions, how can we obtain the execution results within 100 milliseconds?
select * from R inner join S on S.A = R.A inner join T on T.B = R.B
where R.condition_1 and S.condition_2 and T.condition_3
order by R.col1 asc , R.col2 desc limit offset, len;Clearly, the process of executing the complex query first, materializing the results, and then computing the Top-K is insufficient to meet performance requirements. The database must be designed with scheduling and scanning mechanisms that automatically identify the correct stopping points, so that once the pagination output requirement is met, the scan is immediately terminated. We need to address several technical challenges:
Next, we will discuss PolarDB-X's optimization for early termination in pagination for complex queries.
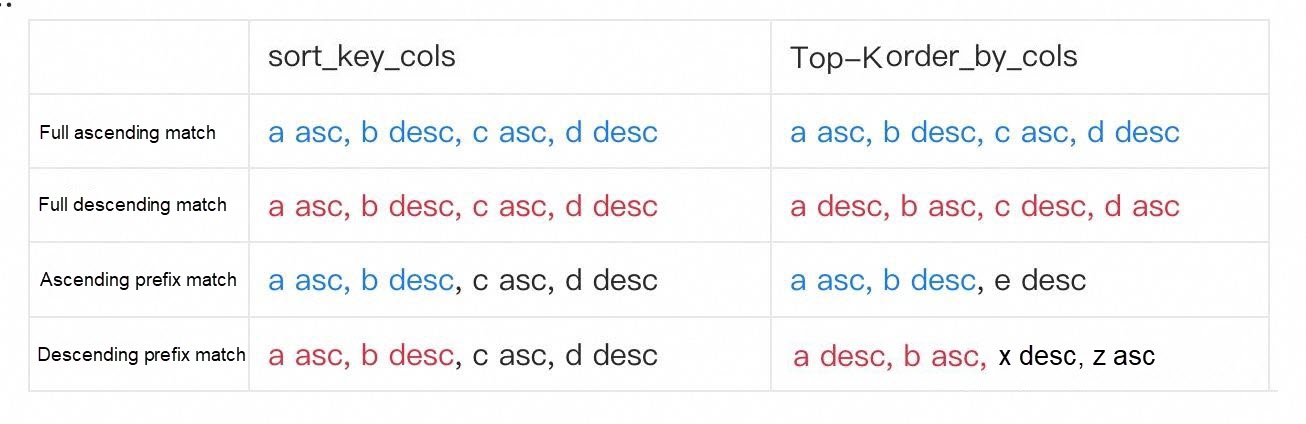
To apply the early termination policy, the system first identifies and matches eligible execution segments. An execution segment must meet all of the following conditions:
1. It must be capable of forming a pipeline.
2. The pipeline must start with a Scan operator and end with a Top-K operator.
3. The ORDER BY columns of the Top-K operator (order_by_cols = (order_by_col1 ASC|DESC, order_by_col2 ASC|DESC, order_by_col3 ASC|DESC, …)) and the sort key of the underlying table scanned by the Scan operator (sort_key_cols = (sort_key_col1 ASC|DESC, sort_key_col2 ASC|DESC, sort_key_col3 ASC|DESC, …)) must satisfy one of the following four relationships:
Example:
For an SQL query initiated by a user, the query is first parsed by the parser, which performs syntax analysis and converts it into an intermediate representation, typically an abstract semantics tree (AST). The AST is then passed to the query optimizer, which selects the execution plan with the lowest cost and generates an execution plan or execution tree. The execution plan provides a detailed description of how the database engine will execute the query, including the order of operations, the algorithms used, and the data structures involved. The database execution engine then executes the query according to the execution plan and returns the results to the user.
For example, in the case of the query discussed in this section, the following tree structure is generated, which means:
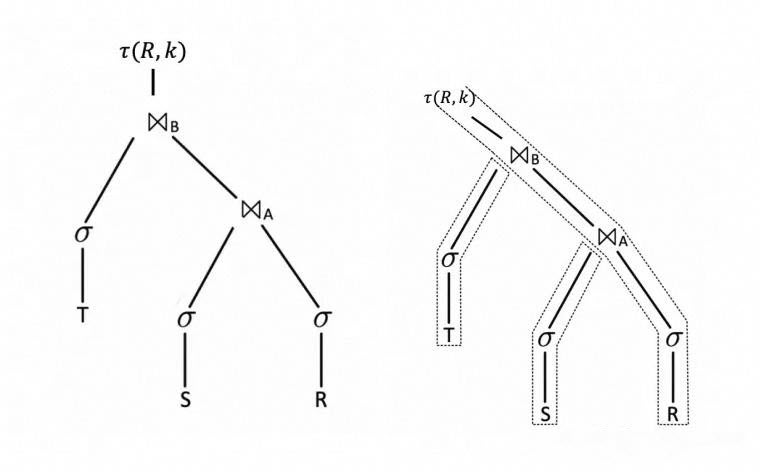
In database systems, a pipeline execution framework (also called an execution pipeline or query pipeline) refers to a policy for organizing and executing the components or operators of a query execution plan in a pipelined manner. Query processing involves multiple steps and a variety of operators, such as join, selection, and projection, each of which may need to process large volumes of data.
Operators can be executed serially, meaning one operator begins only after its predecessor finishes. However, this can be inefficient because downstream operators may remain idle while waiting. By contrast, a pipeline execution framework enables an operator to start processing the upstream operator's output as soon as partial results are available, rather than waiting for the upstream operator to complete processing all input. This approach can significantly improve overall query performance.
The concept of pipeline execution is analogous to instruction pipelining in computer architecture: A downstream stage does not have to wait for the upstream stage to finish processing the entire input before it begins working.
Within a pipeline execution framework, operators are generally classified by their execution behavior into two categories:
1. Blocking execution: An operator must wait until all of its input data has been processed before it can begin execution.
2. Non-blocking execution: An operator can start processing data as soon as it receives output from its upstream operator, without waiting for all input data to be processed.
Pipeline execution substantially improves resource utilization and the degree of parallelism in query processing, because different stages of a query can run concurrently on multiple cores or processors. Most modern database systems, such as PostgreSQL, MySQL, and Oracle, adopt some form of pipeline execution policy to optimize query performance.
This step follows the same concept as in the parallel Top-K implementation. Let's first recall that the Top-K threshold is defined as a value such that, at a given moment, there are more than K elements greater than this threshold. The threshold is greater than or equal to the final Kth largest value (Kth). It evolves dynamically and gradually converges toward Kth over time. Any element smaller than the current threshold cannot appear in the final Top-K result set. Therefore, the Top-K threshold can be used by the Top-K operator during data filtering to exclude data that does not meet the criteria as early as possible.
All parallel operators jointly maintain a shared variable Vk, which represents the currently known global Kth largest value. This value could be a single-column value (val_col) or a vector composed of multiple columns ({val_col1, val_col2, ..., val_colx}). Through the collaboration of different parallel operators, the value of Vk gradually converges toward the true global Kth largest value Kth.
1. Initial state: At the time of Top-K operator initialization, the total number of global elements is zero, so the Kth largest value (Kth) cannot yet be determined.
2. Element count update: Within each node, every time a row is written into a Top-K operator, the total number of elements written across all Top-K operators on that node is updated. This update is atomic, thread-safe, and concurrent.
3. Initialization of Vk value: Once the global total number of elements reaches K, each Top-K operator maintains a min-heap of size K. Then, the heap top elements are collected from all local heaps, and the smallest among them 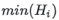is selected as the current global Vk. This completes the initialization of the Vk value.
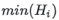represent the heap top (minimum value) of the i-th thread. Then, the global Kth largest value Kth is the minimum among these minimum values 
, which corresponds to the Kth largest value in the overall Top-K candidate set.4. Concurrent Vk updates within a node: After the Vk value is initialized, all parallel operators concurrently and safely update the global Vk. Whenever a value is written into a Top-K operator, the operator compares and potentially updates the global Vk, aiming to raise its value and complete convergence as quickly as possible. The process works in the following way:
In a single-threaded Top-K process, once the heap reaches K elements, its top element naturally serves as the current threshold, and any change to the heap top represents a threshold update. In contrast, under the multi-threaded global Top-K threshold maintenance mechanism described above, multiple threads collaboratively maintain Vk, allowing the threshold to converge toward the final Kth largest value (Kth) more rapidly and to enable earlier pruning of elements that do not meet the Top-K criteria.
For the TPC-H 100GB standard benchmark dataset, experiments were conducted to record the variation of the Top-K threshold during query execution. The query used for testing was SELECT * FROM lineitem ORDER BY l_partkey DESC LIMIT 10000, 10. The changes in the threshold were measured and compared between the following configurations: single-threaded execution, where each thread updates its local threshold independently; multi-threaded execution with 2, 4, and 8 threads, where all threads collaboratively maintain a global threshold. The diagram below shows the results.
(If the SQL query is ORDER BY l_partkey ASC LIMIT 10000, 10, the curve will gradually decrease from the maximum value and converge toward a smaller Kth value.)
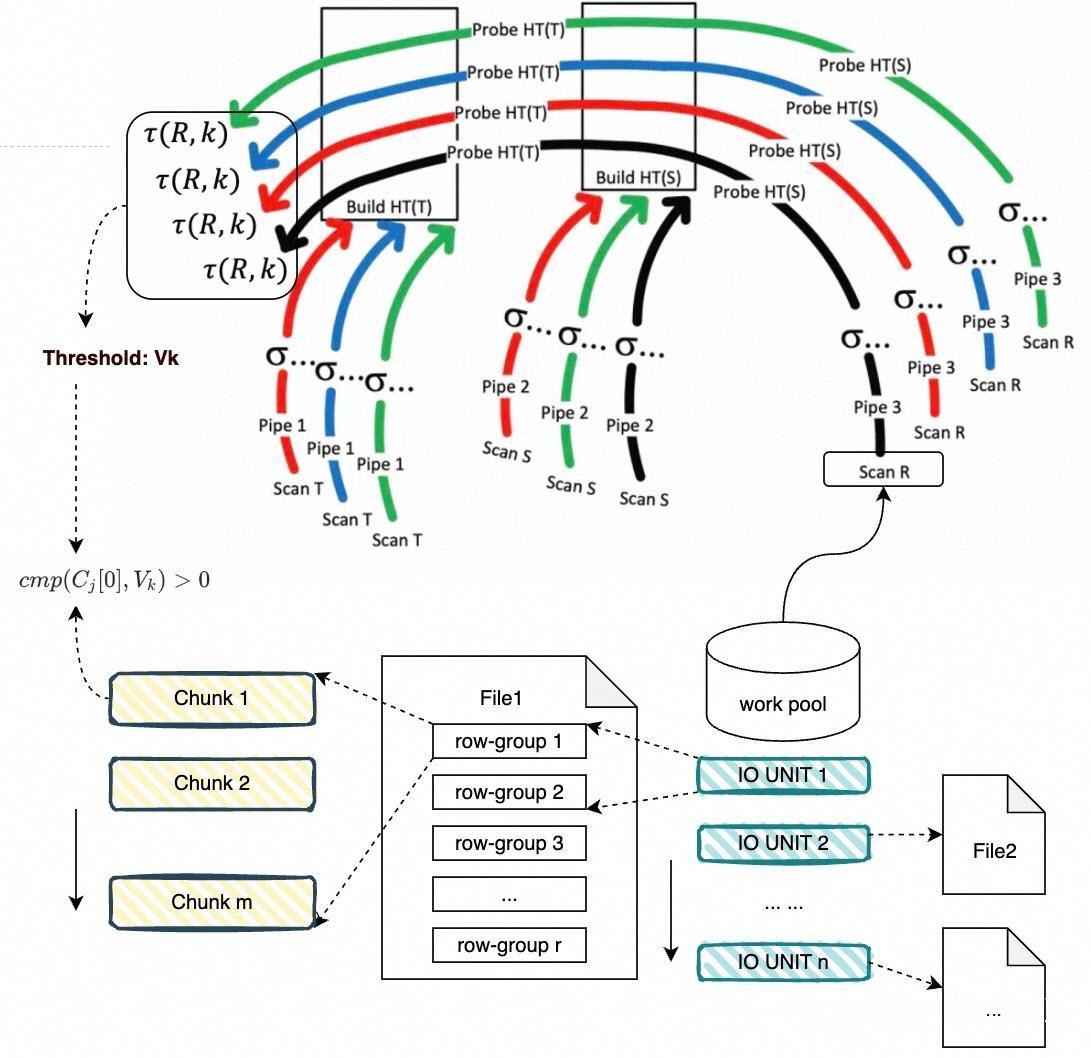
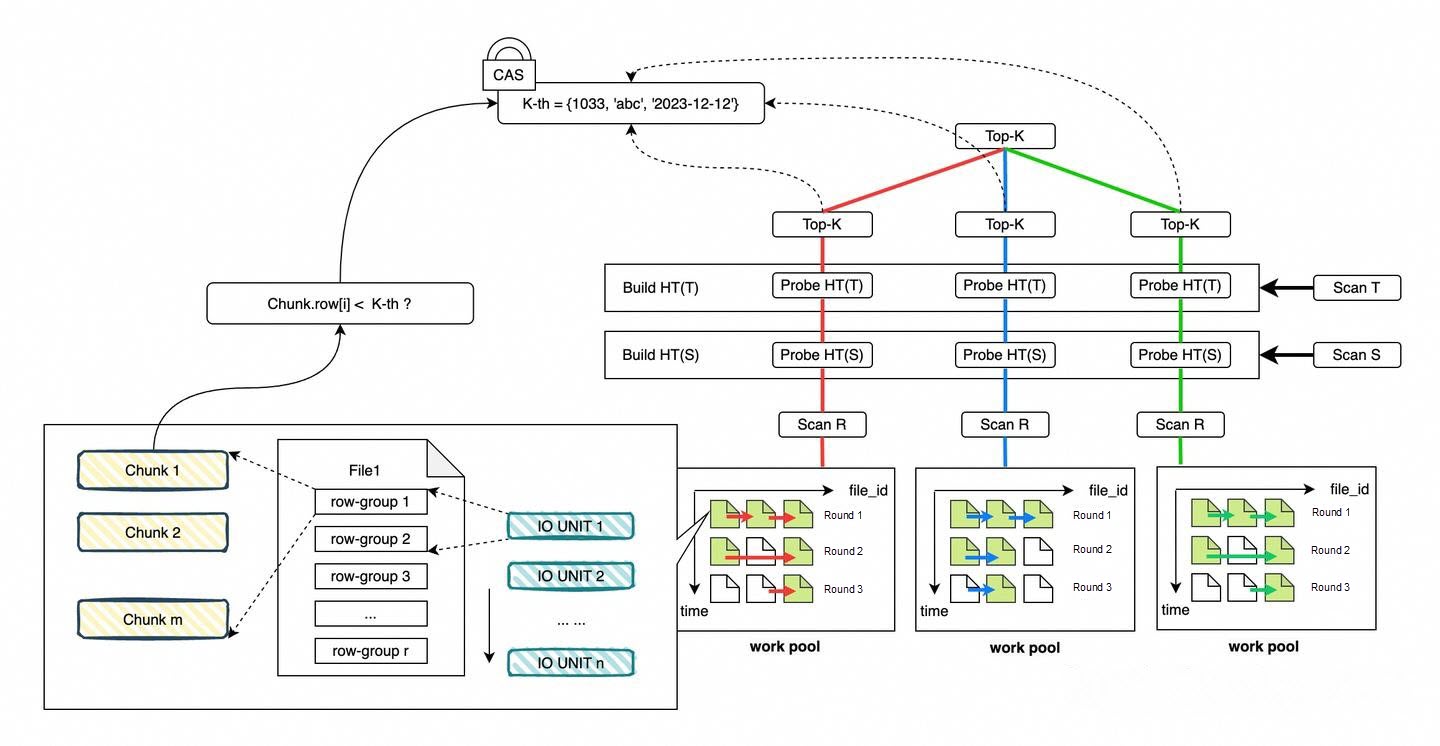
To fully leverage the Top-K threshold for early termination during file reads, each thread maintains a work pool to manage its scan tasks. Let the file set be F:
Each thread retrieves scan tasks from its own work pool. Within a thread, an interleaved file read policy is employed to avoid processing a single file sequentially. This prevents large amounts of data that would not contribute to Join or Filter results from being read and subsequently forming Top-K inputs and thresholds.
The following specific policy is used:
1. Iterate over the file set F in a loop. After completing one round, start another iteration.
2. For each file encountered during iteration, extract the next I/O unit sequentially for execution, positioned immediately after the previous I/O unit in the file. Specifically:
3. For each file, only one I/O unit or task is selected per iteration before moving on to the next file.
4. When a file has no remaining I/O tasks, remove it from the file set F.
5. Continue until there are no files left in the set, at which point the iteration terminates.
This interleaved read policy ensures that, when processing multiple files, a single thread can terminate reading for each file as early as possible based on the current Top-K threshold.
Design of I/O units:
By appropriately setting m and r, each I/O unit can approximately meet the target row count, thereby improving the efficiency of Top-K data collection.
Each row-group contains multiple chunks, and each chunk includes multiple columns with 1,024 rows. To extract the values of the ordering columns from a chunk, the corresponding I/O unit of the row-group must be read into memory, after which the column data is parsed.
By leveraging the global threshold, early termination during file scanning can be achieved to reduce unnecessary I/O operations and computational overhead. The following specific policy is used:
If the Top-K ordering columns (order_by_cols) and the file sort keys (sort_key_cols) have a full ascending match or an ascending prefix match relationship, extraction within each row-group starts from the first chunk, in sequential order:
Where, 
represents the j-th chunk in the row-group, and each chunk contains 1,024 rows. The early termination condition is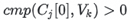 
Cj[0] represents the first row in the j-th chunk.
The following comparison algorithm is defined:
• Full ascending match relationship: Compare each column sequentially until the first non-zero comparison result is obtained, and then return that result.
• Ascending prefix match relationship: Compare only the columns in the prefix sequentially until the first non-zero comparison result is obtained, and then return that result.
Once the termination condition is met, all remaining chunks within the row-group, as well as all subsequent row-groups in the file, are skipped. No further I/O, extraction, or computation is performed. The file read task is then terminated and removed from the work pool.
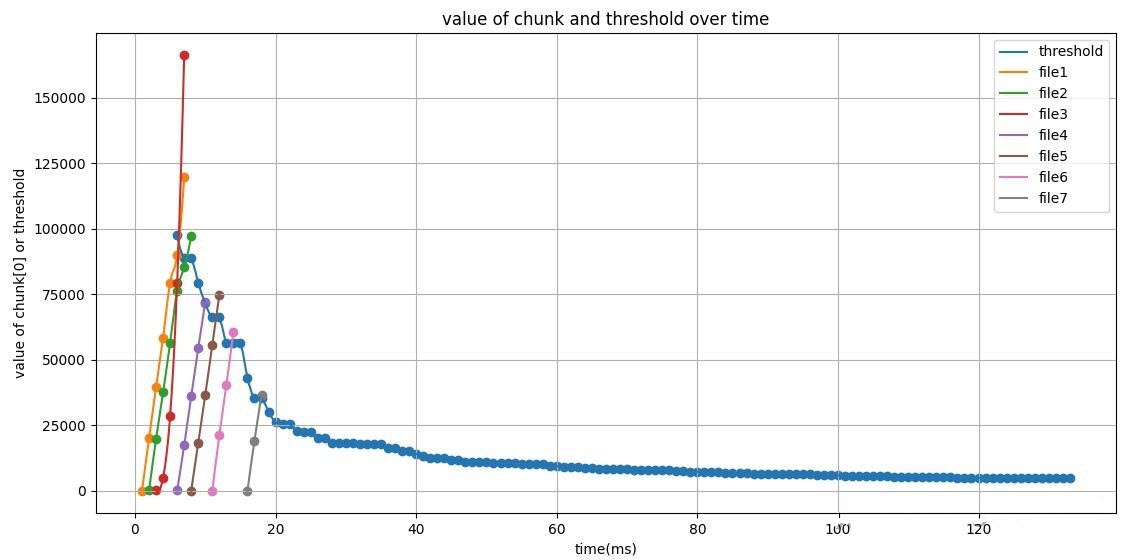
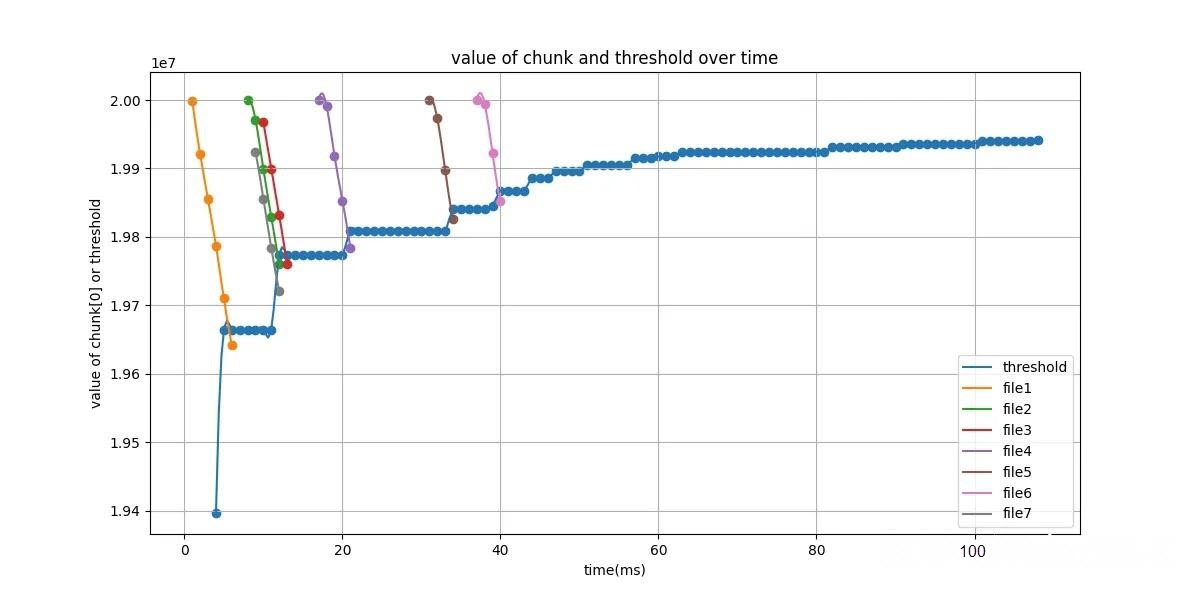
The diagram below illustrates, for the TPC-H 100GB test dataset under full ascending match and ascending prefix match scenarios, the following during pagination execution (SELECT * FROM partsupp ORDER BY ps_partkey LIMIT 10000, 5): the variation of the Top-K threshold over time and the first row of each chunk (chunk[0]) produced by different files within the thread over time. If the value of chunk[0] exceeds the current Top-K threshold Vk, the reading process for that file is immediately terminated.
If the Top-K ordering columns (order_by_cols) and the file sort keys (sort_key_cols) have a full descending match or a descending prefix match relationship, extraction within each row-group starts from the last chunk, in sequential order: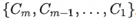 
. Where, C_j represents the j-th chunk in the row-group, and each chunk contains 1,024 rows. The early termination condition is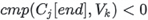 
Cj[end] represents the last row in the j-th chunk.
The following comparison algorithm is defined:
• Full descending match relationship: Compare each column sequentially until the first non-zero comparison result is obtained, and then return that result.
• Descending prefix match relationship: Compare only the columns in the prefix sequentially until the first non-zero comparison result is obtained, and then return that result.
Once the termination condition is met, all remaining chunks within the row-group, as well as all subsequent row-groups in the file, are skipped. No further I/O, extraction, or computation is performed. The file read task is then terminated and removed from the work pool.
The diagram below illustrates, for the TPC-H 100GB test dataset under full ascending match and ascending prefix match scenarios, the following during pagination execution (SELECT * FROM partsupp ORDER BY ps_partkey DESC LIMIT 10000, 5;): the variation of the Top-K threshold over time and the last row of each chunk (chunk[end]) produced by different files within the thread over time. If the value of chunk[end] is less than the current Top-K threshold Vk, the reading process for that file is immediately terminated.
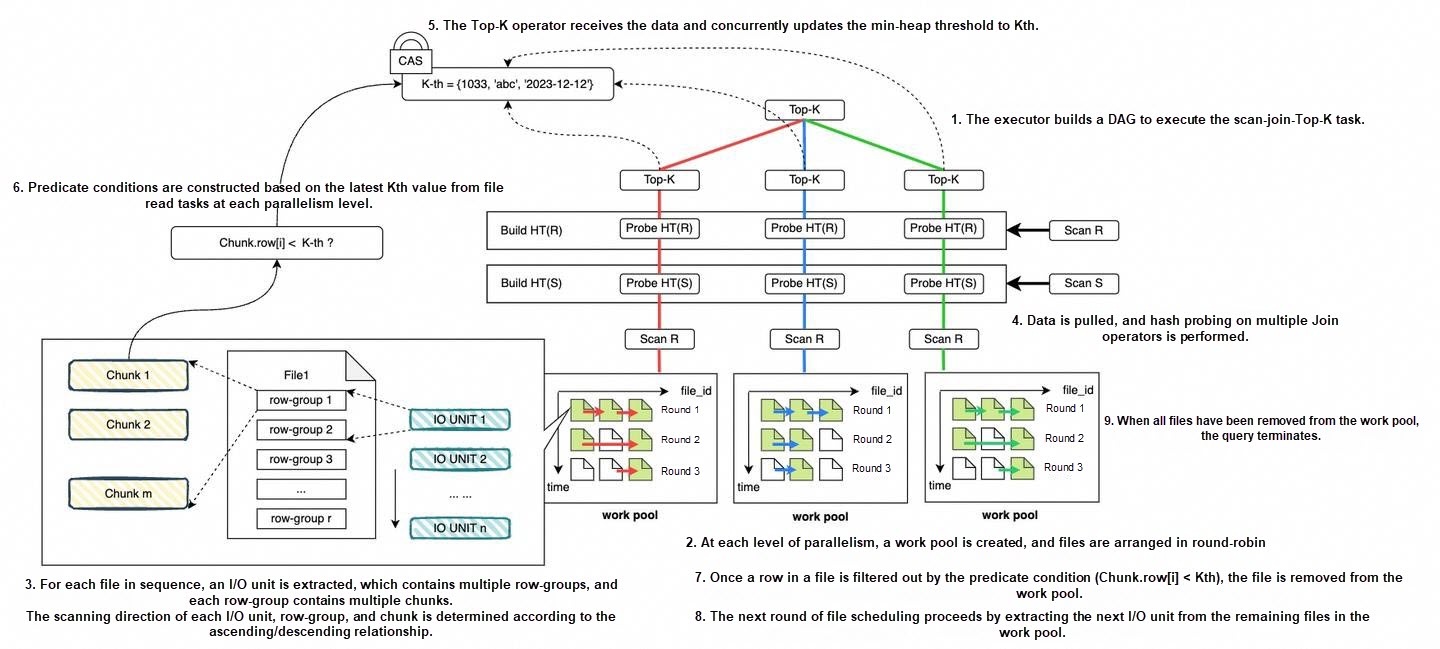
Based on the steps described above, we can summarize how the PolarDB-X executor handles complex query pagination:
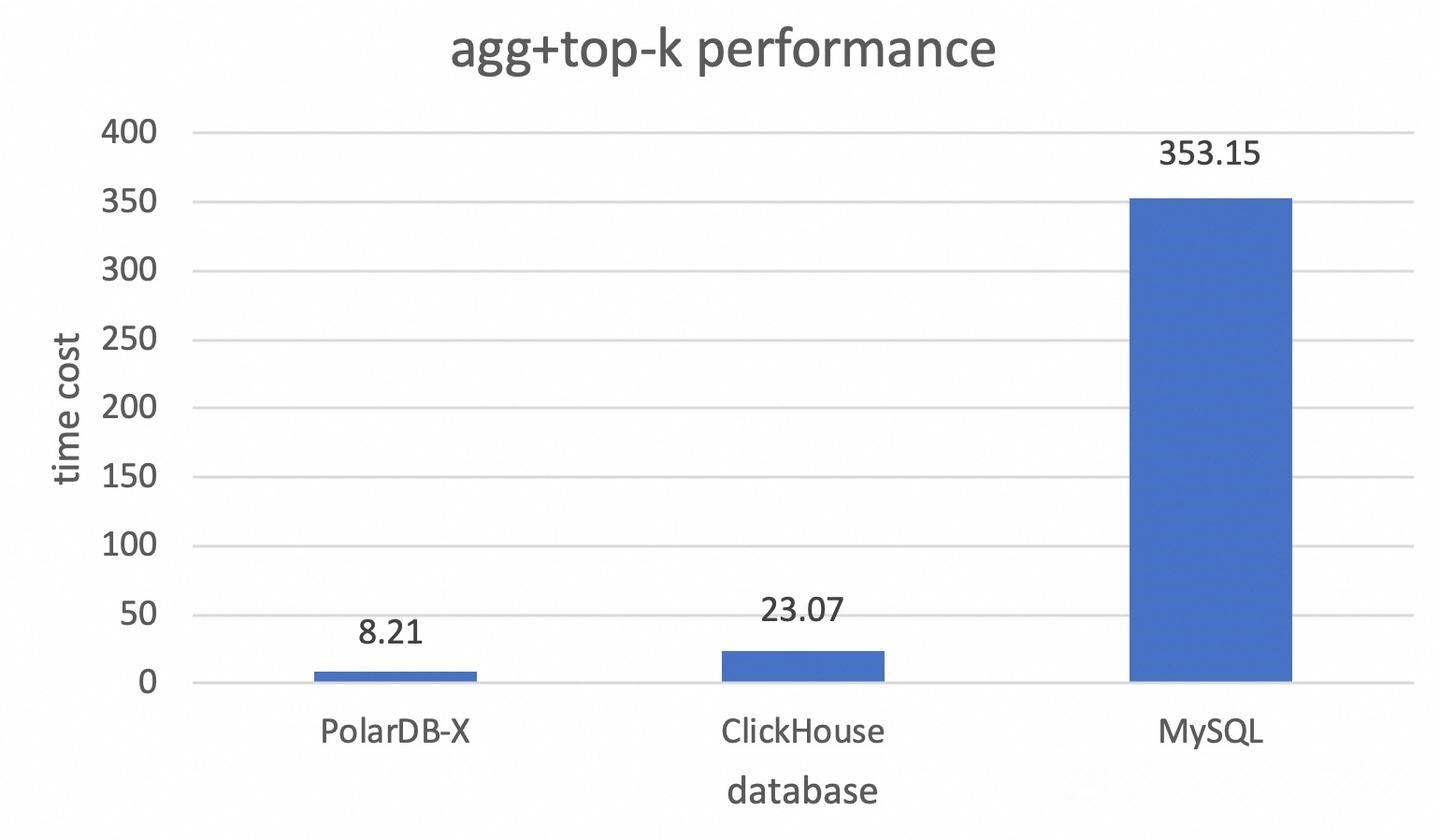
• TPC-H 100GB test dataset
• Specification: 2×16-core and 64 GB memory
• SQL: select sum(l_quantity),l_orderkey from lineitem group by l_orderkey order by sum(l_quantity) desc limit 1000000, 10;
• Test results
| PolarDB-X | ClickHouse | MySQL |
|---|---|---|
| 8.21 sec | 23.07 sec | 353.15 sec |
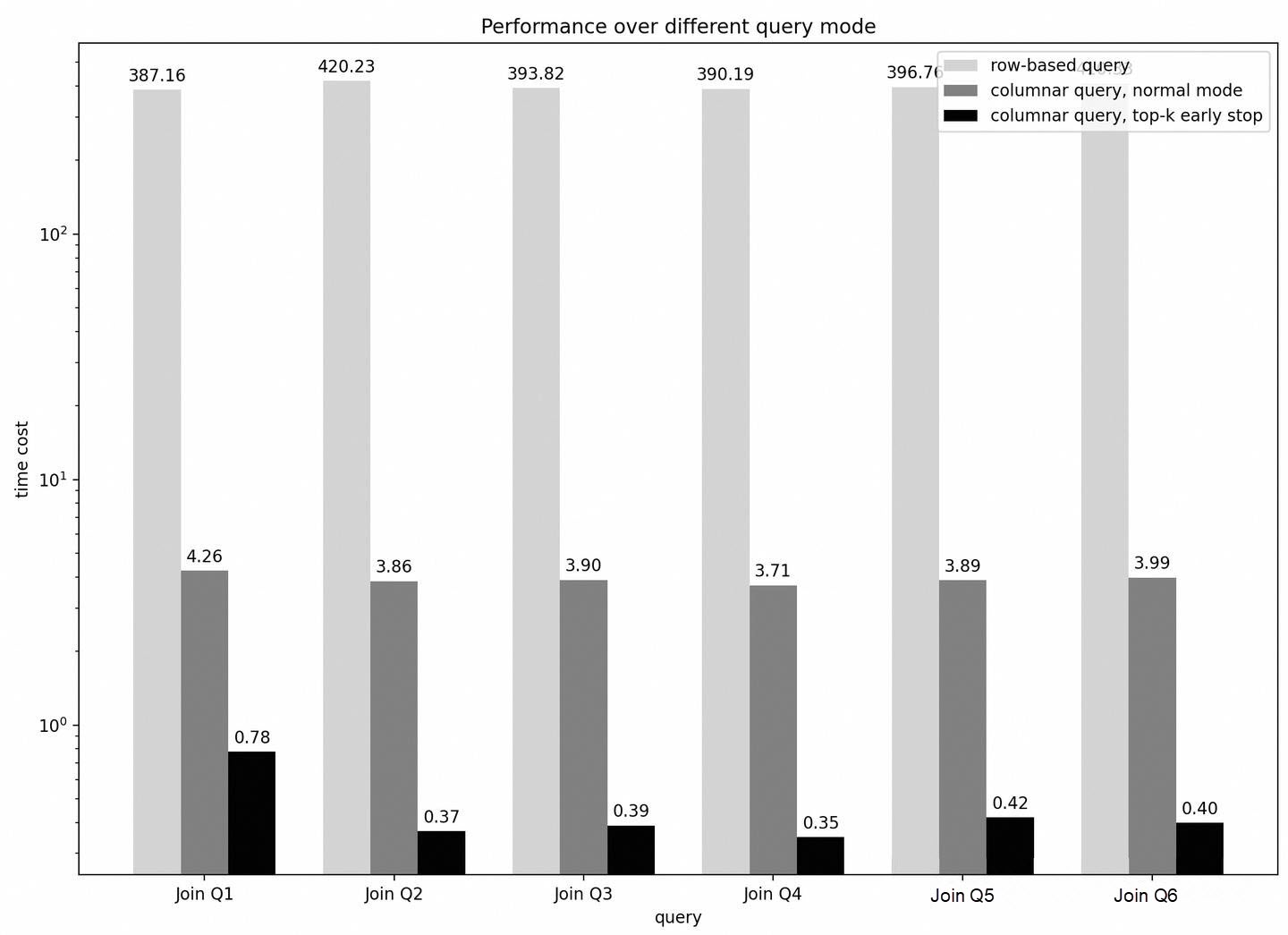
The diagram below presents test results of six different multi-table join query scenarios.
| No. | SQL |
|---|---|
| Q1 | select l_shipdate,l_orderkey from lineitem, supplier where lineitem.l_suppkey = supplier.s_suppkey order by l_shipdate limit 20000,10; |
| Q2 | select l_shipdate,l_orderkey from lineitem, supplier where lineitem.l_suppkey = supplier.s_suppkey order by l_shipdate, l_orderkey limit 20000,10; |
| Q3 | select l_shipdate,l_orderkey from lineitem, supplier where lineitem.l_suppkey = supplier.s_suppkey order by l_shipdate, l_orderkey desc limit 20000,10; |
| Q4 | select l_shipdate,l_orderkey from lineitem, supplier where lineitem.l_suppkey = supplier.s_suppkey order by l_shipdate desc limit 20000,10; |
| Q5 | select l_shipdate,l_orderkey from lineitem, supplier where lineitem.l_suppkey = supplier.s_suppkey order by l_shipdate desc, l_orderkey limit 20000,10; |
| Q6 | select l_shipdate,l_orderkey from lineitem, supplier where lineitem.l_suppkey = supplier.s_suppkey order by l_shipdate desc, l_orderkey desc limit 20000,10; |
Test results
PolarDB-X employs a series of designs to enhance the performance of Top-K queries and pagination queries of large-scale data. The key points described in this article include:
Architecture of multi-level parallel Top-K operators
Multi-threaded collaborative Kth value updates
Tight coordination between upstream and downstream operators
Internal execution flow of Top-K operators
Threshold-based early termination of file scheduling policies
These designs enable PolarDB-X to return Top-K results efficiently and with low latency to meet performance requirements when dealing with complex queries and large-scale datasets.
[Infographic] Highlights | Database New Features in October 2025
ApsaraDB - March 19, 2025
ApsaraDB - November 18, 2025
ApsaraDB - April 10, 2024
Alibaba Cloud Community - September 10, 2024
ApsaraDB - October 24, 2025
ApsaraDB - March 26, 2025
PolarDB for PostgreSQL
Alibaba Cloud PolarDB for PostgreSQL is an in-house relational database service 100% compatible with PostgreSQL and highly compatible with the Oracle syntax.
Learn More
PolarDB for Xscale
Alibaba Cloud PolarDB for Xscale (PolarDB-X) is a cloud-native high-performance distributed database service independently developed by Alibaba Cloud.
Learn More
PolarDB for MySQL
Alibaba Cloud PolarDB for MySQL is a cloud-native relational database service 100% compatible with MySQL.
Learn More
Elastic High Performance Computing Solution
High Performance Computing (HPC) and AI technology helps scientific research institutions to perform viral gene sequencing, conduct new drug research and development, and shorten the research and development cycle.
Learn MoreMore Posts by ApsaraDB
