The Use of Vector Rotation in a Two-Dimensional Space

Vector operation is the mathematical basis of computer graphics, and the rotation of vectors is a common operation of vectors. This article will explain the principle of vector rotation in a two-dimensional space.

We will use the rotate function of Cascading Style Sheets (CSS) to rotate an element in a frontend project. This article will give you a new understanding of rotate.

1. Vector

The vector in the middle of the two dimensions is an array containing two values. One is the x coordinate value, and the other is the y coordinate value.

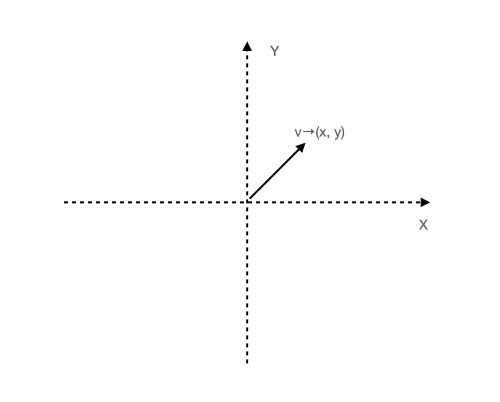
A vector can represent either a point (x, y) or a line from (0,0) to a coordinate point (x, y) called a vector.

2. Rotation of the Vector

The rotation of a vector means to rotate a known vector by a given radian to obtain a new rotated vector, which also means that we use vector and radian to get a new vector by rotation. We describe the process through a pseudo-code:

/**
* v1: raw vector
* v2: new vector after rotation
* rad: rotation radian
*/
const v2 = v1.rotate(rad);

If we want to implement a rotate function to rotate a vector, linear transformation of a matrix can help us.

2.1 Linear Transformation of Matrix

When a matrix and a vector are multiplied, a new vector will be generated (the multiplication of the vector and the matrix describes a motion), and the matrix describes how a two-dimensional space is transformed (rotation, stretching, etc.). The vector is equivalent to an input parameter.

This is similar to how a function works. When a matrix describes that a two-dimensional space is rotated 90° counterclockwise, a new vector rotated 90° counterclockwise will be obtained when any random vector is multiplied with the matrix.

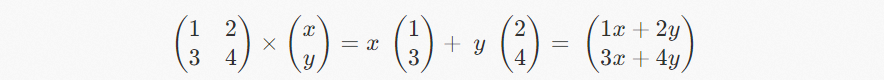
In the formula above, the 2x2 matrix on the left describes how the two-dimensional space is transformed, and the (x, y) on the right is a vector. So, a new vector for the overall calculation process is generated by the matrix and vector through multiplication.

2.1.1 Basis Vector

Why can a 2x2 matrix describe how a two-dimensional space is transformed? This question is critical, so we have a separate section to discuss it.

We can use the transformation of the basis vector to indicate any linear transformation in space, and the number of basis vectors is consistent with the dimensions. For example, basis vectors in a two-dimensional space are two vectors called: i cap and j cap. These two basis vectors have their own x coordinates (1,0) and y coordinates (0,1), so they add up to a 2x2 matrix:

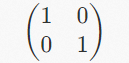
The left column represents the i cap, and the right column represents the j cap. The number above is the x coordinate, and the number below is the y coordinate. The representation in space is shown in the following figure:

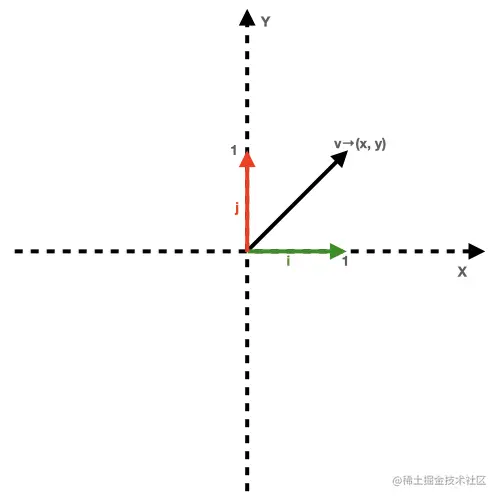
As shown in the figure above, the vector v is obtained by adding together the basis vector i cap and the j cap. Therefore, when the coordinates of the i cap and the j cap change, the vector v will change as well (such as rotating 90° counterclockwise). Then, the matrix value is:

In this case, the 2x2 matrix value is:

The following figure shows the representation in the space:

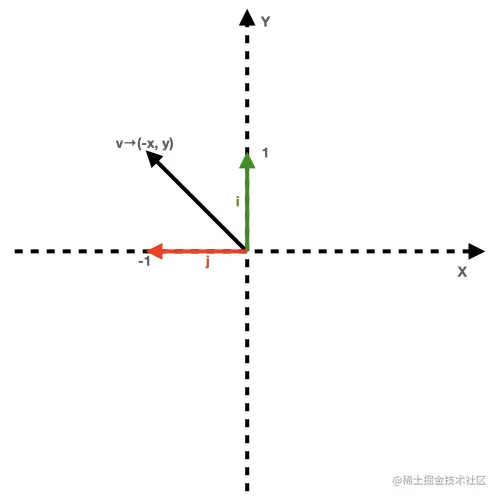
Since the entire space changes linearly, the change of the basis vector is equivalent to the change of any vector, coordinate, and graph in the space.

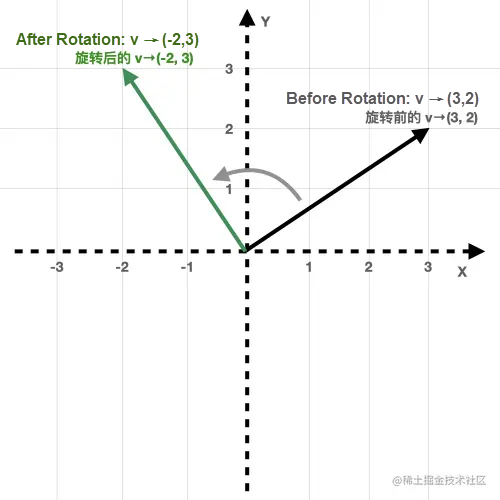
For example, any vector v→(3, 2) in space, multiplied by the matrix above, will give us a new vector that is rotated 90° counterclockwise:

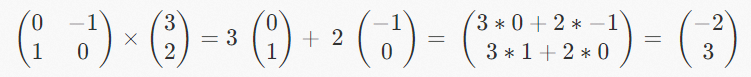
The following figure shows the representation in the space:

2.1.2 Summary

Let's get back to our topic. Now, we know we can obtain new vectors with the matrix and the vector. The vector is known to us, but we don't have the matrix yet. However, we have a radian value, so we should convert the radian into a matrix and then multiply the matrix and vector to obtain the transformed new vector.

2.2 Convert Radian Values into Matrices

This section introduces a method to calculate by radian values with the i cap and j cap coordinates of the basis vector after rotation.

2.2.1 The `i` Cap Coordinates of the Basis Vector After Rotation

Before rotation, the i cap coordinate of the basis vector is (1,0), and the i cap coordinate after rotation is (cosθ, sin θ).

Calculating the coordinates after the rotation of the i cap is calculating the position of the i cap on the x-axis and on the y axis after rotation.

The position of the i cap on the x axis after rotation is equivalent to the projection of the rotated i cap on the i cap before rotation, as shown in the following figure:

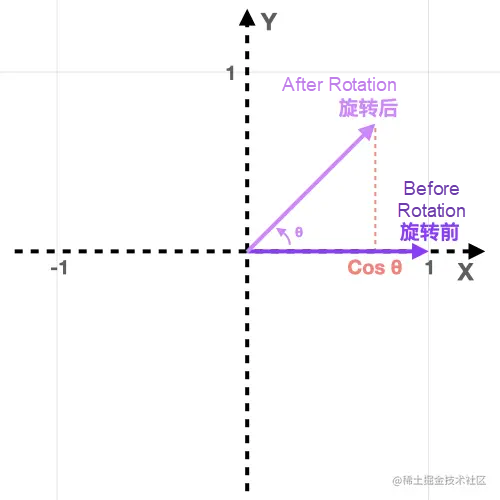
The projection of the vector a on the vector b is equal to the cosine value of the angle between the two vectors multiplied by the length of the vector a. Similarly, the projection of the b on the a is the cosine value multiplied by the length of the vector b.

In our scenario, the cosine value of the i cap after rotation and the i cap clip angle before rotation are multiplied by the length of the i cap. Since the length of the i cap is 1, the cosine value is the coordinate of the i cap on the x axis after rotation.

Now, we obtain the x coordinates of the i cap after rotation: cosθ.

The position of the rotated i cap on the y axis can be calculated by the sine of the included angle. Use the included angle and side length to find the third side of the triangle, and the length of the third side is the position of the i cap on the y axis after rotation, as shown in the following figure:

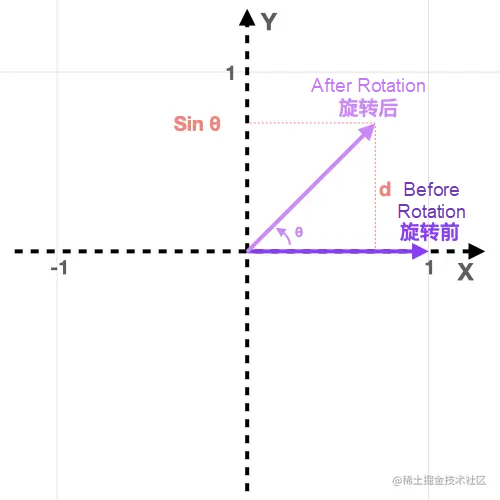
As shown in the figure above, the side d is equal to the position of the rotated i cap on the y axis and is equal to the sinθ. This can be proved with a simple derivation step:

sin θ = opposite side/hypotenuse
It is known that the length of the hypotenuse side is 1 (The length of the i cap is 1, and the length remains unchanged after rotation).
sinθ = d / 1
d / 1 = sinθ
d = sinθ * 1
d = sinθ

Now, we get the y coordinates of the i cap after rotation: sinθ. We also get the complete coordinates of the i cap after rotation:

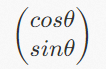
2.2.2 The `j` Cap Coordinates of the Basis Vector after Rotation

The method of obtaining the j cap coordinates after rotation is the same case with the i cap. The coordinates are still obtained by the sine and cosine of the included angle. Before rotation, the coordinates of the basis vector j the cap are (0,1), and the coordinates of the j cap after rotation are (-sinθ, cosθ):

Since the projection of the rotated j cap on the j cap before rotation is cast on the y axis, cosθ obtains the position of the j cap on the y axis after rotation. Similarly, sinθ is the position of the j cap on the x axis after rotation. Since the x axis is less than 0, it is necessary to add a negative sign to the position (sinθ): -sinθ, as shown in the following figure:

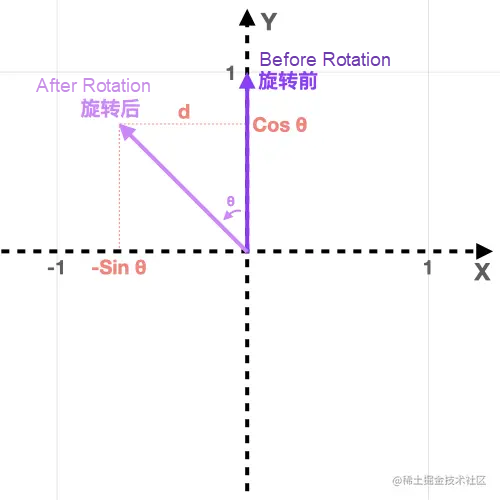
Now, we get the complete coordinates of the j cap after rotation:

2.2.3 Summary

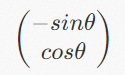
We learned how to calculate the rotation matrix (the i cap and j cap coordinates of the basis vector after rotation) by radian values through the detailed introduction of this section. The rotation matrix is listed below:

2.3 Summary

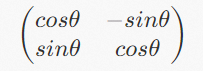
The rotation of a vector means to rotate a known vector by a given radian to obtain a new rotated vector. The matrix describes how a two-dimensional space is transformed. When a matrix and a vector are multiplied, a new vector will be generated. The matrix that describes how the space is transformed can be calculated in radians.

So far, we've learned some theoretical knowledge of vector rotation. The calculation of a complete vector rotation matrix is shown below:

3. Vector Rotation Code Implementation

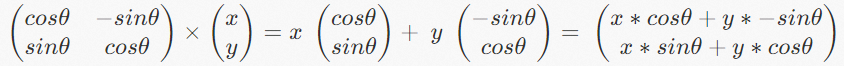
After the detailed introduction in the previous section, we have produced a formula:

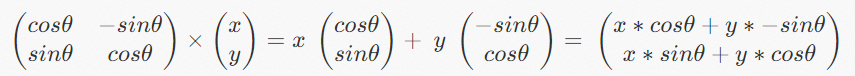
The leftmost 2x2 matrix is calculated using radians and multiplied with the vector on the right to get a new vector. The vector produced in the last step can be used directly in the code. The code is listed below:

/**
* @param {[x, y]} v original vector
* @param {number} rad rotation radians
* @return {[x, y]} new vector after rotation
*/
function rotate(v, rad) {
  const c = Math.cos(rad);
  const s = Math.sin(rad);
  const [x, y] = v;
  
  return [
      x * c + y * -s,
      x * s + y * c
  ];
}

4. Demo Display: A Tree Based on Vector Rotation

This Demo was designed by Yueying.

Community

The Use of Vector Rotation in a Two-Dimensional Space

1. Vector

2. Rotation of the Vector

2.1 Linear Transformation of Matrix

2.1.1 Basis Vector

2.1.2 Summary

2.2 Convert Radian Values into Matrices

2.2.1 The `i` Cap Coordinates of the Basis Vector After Rotation

2.2.2 The `j` Cap Coordinates of the Basis Vector after Rotation

2.2.3 Summary

2.3 Summary

3. Vector Rotation Code Implementation

4. Demo Display: A Tree Based on Vector Rotation

Read previous post:

Read next post:

Alibaba F(x) Team

You may also like

Comments

Alibaba F(x) Team

Related Products

YiDA Low-code Development Platform

mPaaS

Super App Solution for Telcos

Community

The Use of Vector Rotation in a Two-Dimensional Space

1. Vector

2. Rotation of the Vector

2.1 Linear Transformation of Matrix

2.1.1 Basis Vector

2.1.2 Summary

2.2 Convert Radian Values into Matrices

2.2.1 The i Cap Coordinates of the Basis Vector After Rotation

2.2.2 The j Cap Coordinates of the Basis Vector after Rotation

2.2.3 Summary

2.3 Summary

3. Vector Rotation Code Implementation

4. Demo Display: A Tree Based on Vector Rotation

Read previous post:

Read next post:

Alibaba F(x) Team

You may also like

Comments

Alibaba F(x) Team

Related Products

YiDA Low-code Development Platform

mPaaS

Super App Solution for Telcos

2.2.1 The `i` Cap Coordinates of the Basis Vector After Rotation

2.2.2 The `j` Cap Coordinates of the Basis Vector after Rotation