Use the PASE extension to search for vectors in ApsaraDB RDS for PostgreSQL based on the IVFFlat or HNSW algorithm - ApsaraDB RDS

This topic describes how to use the PostgreSQL ANN search extension (PASE) to search for vectors in ApsaraDB RDS for PostgreSQL. PASE works based on the IVFFlat or Hierarchical Navigable Small World (HNSW) algorithm.

Note

The PASE extension is no longer maintained. We recommend that you use the pgvector extension. For more information, see Use the pgvector extension to perform high-dimensional vector similarity searches.

Prerequisites

Your RDS instance runs PostgreSQL 11 or later (except for PostgreSQL 17).

Background information

Representation learning is a typical artificial intelligence (AI) technology in the deep learning discipline. This technology has rapidly developed over the recent years and is used in various business scenarios such as advertising, face scan payment, image recognition, and speech recognition. This technology enables data to be embedded into high-dimensional vectors and allows you to query data by using the vector search approach.

PASE is a high-performance vector search index extension that is developed for PostgreSQL. PASE uses two well-developed, stable, and efficient approximate nearest neighbor (ANN) search algorithms, IVFFlat and HNSW, to query vectors from PostgreSQL databases at a high speed. PASE does not support the extraction or output of feature vectors. You must retrieve the feature vectors of the entities that you want to query. PASE only implements a similarity search among a large number of vectors that are identified based on the retrieved feature vectors.

Intended audience

This topic does not explain the terms related to machine learning in detail. Before you read this topic, you must understand the basics of machine learning and search technologies.

Usage notes

If an index on a table is bloated, you can obtain the size of the indexed data by executing the select pg_relation_size('Index name'); statement. Then, compare the size of the index with the size of the data in the table. If the size of the indexed data is larger than the size of the data in the table and data queries slow down, you must rebuild the index on the table.
An index on a table may be inaccurate after frequent data updates. If you require an accuracy level of 100%, you must rebuild the index on a regular basis.
If you want to create an IVFFlat index on a table by using internal centroids, you must set the clustering_type parameter to 1 and insert some data into the table.
You must use a privileged account to execute the SQL statements that are described in this topic.

Algorithms used by PASE

IVFFlat
IVFFlat is a simplified version of the IVFADC algorithm. IVFFlat is suitable for business scenarios that require high precision but can tolerate up to 100 milliseconds taken for queries. IVFFlat has the following advantages compared with other algorithms:
- If the vector to query is one of the candidate datasets, IVFFlat delivers 100% recall.
- IVFFlat uses a simple structure to create indexes at fast speeds, and the created indexes occupy less storage space.
- You can specify a centroid for clustering and can control precision by reconfiguring parameters.
- You can control the accuracy of IVFFlat by reconfiguring its interpretable parameters.
The following figure shows how IVFFlat works.
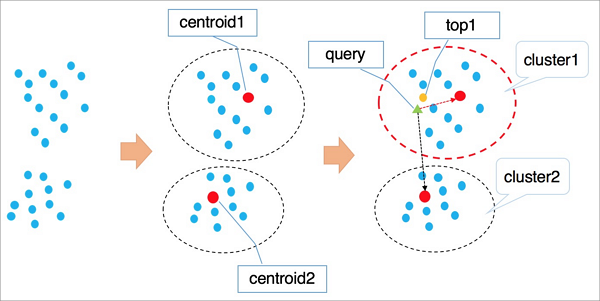
The following procedure describes how IVFFlat works:
1. IVFFlat uses a clustering algorithm such as k-means to divide vectors in the high-dimensional data space into clusters based on implicit clustering properties. Each cluster has a centroid.
2. IVFFlat traverses the centroids of all clusters to identify the n centroids that are nearest to the vector you want to query.
3. IVFFlat traverses and sorts all vectors in the clusters to which the identified n centroids belong. Then, IVFFlat obtains the nearest k vectors.
Note
- When IVFFlat attempts to identify the nearest n centroids, it skips the clusters that are located far away from the vector you want to query. This expedites the query. However, IVFFlat cannot ensure that all the similar k vectors are included in the clusters to which the identified n centroids belong. As a result, precision may decrease. You can use the variable n to control precision. A larger value of n indicates higher precision but more computing workloads.
- In the first phase, IVFFlat works in the same way as IVFADC. The main differences between IVFFlat and IVFADC lie in the second phase. In the second phase, IVFADC uses product quantization to eliminate the need for traversal computing workloads. This expedites the query but decreases precision. IVFFlat implements brute-force search to ensure precision and allows you to control computing workloads.
HNSW
HNSW is a graph-based ANN algorithm that is suitable for queries among tens of millions or more vector datasets. Responses to these queries must be returned within 10 milliseconds or less.
HNSW searches for similar vectors among proximity graph neighbors. If the data volume is large, HNSW significantly improves performance compared with other algorithms. However, HNSW requires the storage of proximity graph neighbors, which occupy storage space. In addition, after the precision of HNSW reaches a specific level, you cannot increase the precision of HNSW by reconfiguring parameters.
The following figure shows how HNSW works.
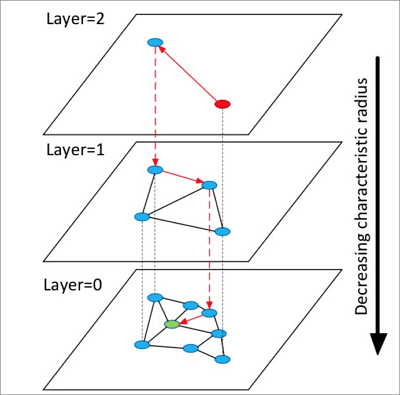
The following procedure describes how HNSW works:
1. HNSW builds a hierarchical structure that consists of multiple layers, which are also called graphs. Each layer is a panorama and skips list of its lower layer.
2. HNSW randomly selects an element from the top layer to start a search.
3. HNSW identifies the neighbors of the selected element and adds the identified neighbors to a fixed-length dynamic list based on the distances of the identified neighbors to the selected element. HNSW continues to identify the neighbors of each neighbor that is included in the list and adds the identified neighbors to the list. Every time when HNSW adds a neighbor to the list, HNSW re-sorts the neighbors in the list and retains only the first k neighbors. If the list changes, HNSW continues to search until the list reaches the final state. Then, HNSW uses the first element in the list as the start for a search in the lower layer.
4. HNSW repeats the third step until it complete a search in the bottom layer.
Note
HNSW constructs a multi-layer structure by using the Navigable Small World (NSW) algorithm that is designed to construct single-layer structures. The employment of an approach for selecting proximity graph neighbors enables HNSW to deliver higher query speedup than clustering algorithms.

IVFFlat and HNSW each are suitable for specific business scenarios. For example, IVFFlat is suitable for image comparison at high precision, and HNSW is suitable for searches with recommended recall.

PASE usage

Procedure

Execute the following statement to create PASE:
```
CREATE EXTENSION pase;
```
Use one of the following construction methods to calculate vector similarity:
- PASE-type-based construction
  Example:
```
SELECT ARRAY[2, 1, 1]::float4[] <?> pase(ARRAY[3, 1, 1]::float4[]) AS distance;
SELECT ARRAY[2, 1, 1]::float4[] <?> pase(ARRAY[3, 1, 1]::float4[], 0) AS distance;
SELECT ARRAY[2, 1, 1]::float4[] <?> pase(ARRAY[3, 1, 1]::float4[], 0, 1) AS distance;
```
  Note
  - <?> is a PASE-type operator, which is used to calculate the similarity between the vectors to the left and right of a specific element. The vector to the left must use the float4[] data type, and the vector to the right must use the PASE data type.
  - The PASE data type is defined in PASE. You can construct data of the PASE type based on the preceding statements. Take the float4[], 0, 1 part in the preceding third statement as an example. The first parameter specifies the vector to the right with the float4[] data type. The second parameter does not serve a special purpose and can be set to 0. The third parameter specifies the similarity calculation method, where the value 0 represents the Euclidean distance method and the value 1 represents the dot product method. A dot product is also called an inner product.
  - The vector to the left must have the same number of dimensions as the vector to the right. Otherwise, the system reports similarity calculation errors.
- String-based construction
  Example:
```
SELECT ARRAY[2, 1, 1]::float4[] <?> '3,1,1'::pase AS distance;
SELECT ARRAY[2, 1, 1]::float4[] <?> '3,1,1:0'::pase AS distance;
SELECT ARRAY[2, 1, 1]::float4[] <?> '3,1,1:0:1'::pase AS distance;
```
  Note
  The string-based construction method differs from the PASE-type-based construction in the following aspect: The string-based construction method uses colons (:) to separate parameters. Take the 3,1,1:0:1 part in the preceding third statement as an example: The first parameter specifies the vector to the right. The second parameter does not serve a special purpose and can be set to 0. The third parameter specifies the similarity calculation method, where the value 0 represents the Euclidean distance method and the value 1 represents the dot product method. A dot product is also called an inner product.

Use IVFFlat or HNSW to create an index.

Note

If you use the Euclidean distance method to calculate a vector similarity, the original vector does not need to be processed. If you use the dot product or the cosine method to calculate a vector similarity, the original vector must be normalized. For example, if the original vector is 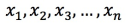, it must comply with the following formula: 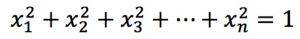. In this example, the dot product is the same as the cosine value.

IVFFlat

CREATE INDEX ivfflat_idx ON table_name
USING
  pase_ivfflat(column_name)
WITH
  (clustering_type = 1, distance_type = 0, dimension = 256, base64_encoded = 0, clustering_params = "10,100");

The following table describes the parameters in the IVFFlat index.

Parameter	Description
clustering_type	The type of clustering operation that IVFFlat performs on vectors. This parameter is required. Valid values: 0: external clustering. An external centroid file is loaded. This file is specified by the clustering_params parameter. 1: internal clustering. The k-means clustering algorithm is used. This algorithm is specified by the clustering_params parameter. If you are using PASE for the first time, we recommend that you select internal clustering.
distance_type	The method that is used to calculate vector similarity. Default value: 0. Valid values: 0: Euclidean distance. 1: dot product. This method requires the normalization of vectors. The order of dot products is opposite to the order of Euclidean distances. ApsaraDB RDS for PostgreSQL supports only the Euclidean distance method. Dot products can be calculated by using the methods that are described in Appendix only after vectors are normalized.
dimension	The number of dimensions. This parameter is required. The maximum value of this parameter is 512.
base64_encoded	Specifies whether to use Base64 encoding. Default value: 0. Valid values: 0: uses the float4[] data type to represent the vector type. 1: uses the Base64-encoded float[] data type to represent the vector type.
clustering_params	For external clustering, this parameter specifies the directory of the external centroid file that you want to use. For internal clustering, this parameter specifies the clustering algorithm that you want to use. The value of this parameter is in the following format `clustering_sample_ratio,k`. This parameter is required. clustering_sample_ratio: the sampling fraction with 1000 as the denominator. The value of this field is an integer within the `(0,1000]` range. For example, if you set this field to 1, the system samples data from the dynamic list based on the 1:1000 sampling ratio before it performs k-means clustering. A larger value indicates higher query accuracy but slower index creation. We recommend that the total number of data records sampled do not exceed 100,000. k: the number of centroids. A larger value indicates higher query accuracy but slower index creation. We recommend that you set this field to a value within the [100, 1000] range.

HNSW

CREATE INDEX hnsw_idx ON table_name
USING
  pase_hnsw(column_name)
WITH
  (dim = 256, base_nb_num = 16, ef_build = 40, ef_search = 200, base64_encoded = 0);

The following table describes the parameters in the HNSW index.

Parameter	Description
dim	The number of dimensions. This parameter is required. Valid values: `[8,512]`.
base_nb_num	The number of neighbors that you want to identify for an element. This parameter is required. A larger value indicates higher query accuracy, but slower index creation and more storage occupied. We recommend that you set this parameter to a value in the `[16,128]` range.
ef_build	The heap length that you want to use during index creation. This parameter is required. A longer heap length indicates higher query accuracy but slower index creation. We recommend that you set this parameter to a value within the `[40, 400]` range.
ef_search	The heap length that you want to use during a query. This parameter is required. A longer heap length indicates higher query accuracy but poorer query performance. Valid values: `[10,400]`.
base64_encoded	Specifies whether to use Base64 encoding. Default value: 0. Valid values: 0: uses the float4[] data type to represent the vector type. 1: uses the Base64-encoded float[] data type to represent the vector type.

Use one of the following indexes to query a vector:
- IVFFlat index
```
SELECT id, vector <#> '1,1,1'::pase as distance
FROM table_name
ORDER BY
vector <#> '1,1,1:10:0'::pase
ASC LIMIT 10;
```
  Note
  - <#> is an operator that is used by IVFFlat indexes.
  - You must execute the ORDER BY statement to make an IVFFlat index take effect. An IVFFlat index allows vectors to be sorted in ascending order.
  - The PASE data type requires three parameters to specify a vector. These parameters are separated by colons (:). For example, 1,1,1:10:0 includes three parameters. The first parameter specifies the vector to query. The second parameter specifies the query efficiency of IVFFlat with a value range of (0,1000], in which a larger value indicates higher query accuracy but poorer query performance. We recommend that you configure this parameter based on your business requirements. The third parameter specifies the vector similarity calculation method, where the value 0 represents the Euclidean distance method and the value 1 represents the dot product method. A dot product is also called an inner product. The dot product method requires the normalization of vectors. The order of dot products is opposite to the order of Euclidean distances.
- HNSW
```
SELECT id, vector <?> '1,1,1'::pase as distance
FROM table_name
ORDER BY
vector <?> '1,1,1:100:0'::pase
ASC LIMIT 10;
```
  Note
  - <?> is an operator that is used by the HNSW index.
  - You must execute the ORDER BY statement to make an HNSW index take effect. An HNSW index allows vectors to be sorted in ascending order.
  - The PASE data type requires three parameters to specify a vector. These parameters are separated by colons (:). For example, 1,1,1:100:0 includes three parameters. The first parameter specifies the vector to query. The second parameter specifies the query efficiency of HNSW with a value range of (0, ∞), in which a larger value indicates higher query accuracy but poorer query performance. We recommend that you set the second parameter to 40 and then test the value by small increases until you find the most suitable value for your business. The third parameter specifies the vector similarity calculation method, where the value 0 represents the Euclidean distance method and the value 1 represents the dot product method. A dot product is also called an inner product. The dot product method requires the normalization of vectors. The order of dot products is opposite to the order of Euclidean distances.

Example

Use the IVFFlat index to query a vector.

Execute the following statement to create PASE:
```
CREATE EXTENSION pase;
```

Create a test table and insert test data into the table.

Execute the following statement to create a test table:

CREATE TABLE vectors_table ( id SERIAL PRIMARY KEY, vector float4[] NOT NULL );

Insert test data into the table.

INSERT INTO vectors_table (vector) VALUES ('{1.0, 0.0, 0.0}'), ('{0.0, 1.0, 0.0}'), ('{0.0, 0.0, 1.0}'), ('{0.0, 0.5, 0.0}'), ('{0.0, 0.5, 0.0}'), ('{0.0, 0.6, 0.0}'), ('{0.0, 0.7, 0.0}'), ('{0.0, 0.8, 0.0}'), ('{0.0, 0.0, 0.0}');

Use the IVFFlat algorithm to create an index.

CREATE INDEX ivfflat_idx ON vectors_table
USING
  pase_ivfflat(vector)
WITH
  (clustering_type = 1, distance_type = 0, dimension = 3, base64_encoded = 0, clustering_params = "10,100");

Use the IVFFlat index to query a vector.

SELECT id, vector <#> '1,1,1'::pase as distance
FROM vectors_table
ORDER BY
vector <#> '1,1,1:10:0'::pase
ASC LIMIT 10;

Appendix

Calculate the dot product of a vector.

For this example, use an HNSW index to create a function:

CREATE OR REPLACE FUNCTION inner_product_search(query_vector text, ef integer, k integer, table_name text) RETURNS TABLE (id integer, uid text, distance float4) AS $$
BEGIN
    RETURN QUERY EXECUTE format('
    select a.id, a.vector <?> pase(ARRAY[%s], %s, 1) AS distance from 
    (SELECT id, vector FROM %s ORDER BY vector <?> pase(ARRAY[%s], %s, 0) ASC LIMIT %s) a
    ORDER BY distance DESC;', query_vector, ef,  table_name,  query_vector, ef, k);
END
$$
LANGUAGE plpgsql;

Note

The dot product of a normalized vector is the same as its cosine value. Therefore, you can also follow this example to calculate the cosine value of a vector

Create an IVFFlat index from an external centroid file.
This is an advanced feature. You must upload an external centroid file to the specified directory of the server and use this file to create an IVFFlat index. For more information, see the parameters of the IVFFlat index. This file is in the following format:
```
Number of dimensions|Number of centroids|Centroid vector dataset
```
Example:
```
3|2|1,1,1,2,2,2
```

References

Product Quantization for Nearest Neighbor Search
Herv ́e J ́egou, Matthijs Douze, Cordelia Schmid. Product quantization for nearest neighbor search.
Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs
Yu.A.Malkov, D.A.Yashunin. Efficient and robust approximate nearest neighbor search using Hierarchical Navigable Small World graphs.