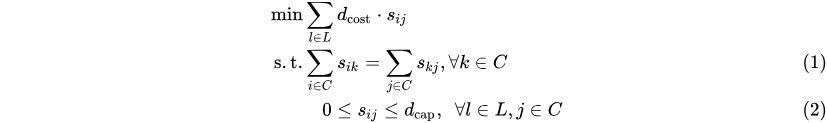All Products
Search

This Product

    Optimization Solver:Logistics: Network flow problem for cost minimization

    Document Center

    Optimization Solver:Logistics: Network flow problem for cost minimization

    Last Updated:Jan 12, 2026

    Industrial background

    Logistics is the key to supply chain management, and it often involves multiple activities such as transportation, warehousing, loading and unloading, and distribution. How can transportation plans be reasonably arranged to improve the efficiency and reliability of cargo transportation and reduce logistics costs? This optimization problem can be modeled and solved using mathematical programming methods.

    For example, a company needs to ship products from its factory to a distribution center and then to various warehouses. The shipping cost is different for each warehouse, and each route has a capacity limit. The goal is to create a transportation plan that minimizes the total cost.

    image.png

    Business research, data quantification, and mathematical modeling

    When using optimization techniques, you need to investigate the needs of business in more detail, organize the relevant business logic and data, and quantify them. Then, you can use a mathematical programming method for modeling.

    For more details, see . This section lists only the related mathematical formula.

    image.svg

    In the preceding formula, s represents the goods that are available at each site, d represents the goods that are needed at each site, i and j represent the start and end sites of a transportation line, and k represents the intermediate site.

    Constraints on the preceding formula:

    1. The sum of the goods available at a site plus the goods shipped into that site is equal to the sum of the goods needed at that site plus the goods shipped out of that site.

    2. Each transportation line has an upper limit on delivery capacity.

    Source code

    MindOpt can be called from multiple programming and modeling languages. The following is an example:

    Invoking the MindOpt APL modeling language

    Source code for MindOpt APL (you can access to perform a dry run): 

    ##====Source code for MindOpt APL====

clear model;

# Modeling -------
# net2.mapl
# Data
set CITIES := {"HN", "NE", "SE", "LN", "JL", "HLJ", "JS", "ZJ"} ;

set LINKS := {<"HN", "NE">, <"HN", "SE">, <"NE", "LN">, <"NE","JL">, <"NE","HLJ">, <"SE","LN">, <"SE","JL">, <"SE", "JS">, <"SE", "ZJ">};

param supply[CITIES] := <"HN"> 450 default 0;

param demand[CITIES] := <"JS"> 90,  <"ZJ"> 70, <"JL"> 120,  <"LN"> 120, <"HLJ"> 50 default 0;

set C := {"cost", "capacity"};

param data[LINKS * C] :=
            | "cost",  "capacity"|
|"HN", "NE" |    3.5,    250    |
|"HN", "SE" |    2.5,    250    |
|"NE", "LN" |    1.5,    100    |
|"NE", "JL" |    1.7,    100    |
|"NE", "HLJ"|    2.0,    100    |
|"SE", "LN" |    2.6,    100    |
|"SE", "JL" |    2.7,    100    |
|"SE", "JS" |    1.3,    100    |
|"SE", "ZJ" |    1.5,    100    |;

# Check whether the data is correct.
forall {<i> in CITIES } check supply[i] >= 0;
forall {<i> in CITIES } check demand[i] >= 0;
check sum {<i> in CITIES } supply[i] >= sum {<j> in CITIES} demand[j]; # The supply exceeds the demand.

# Model
var Ship[<i, j> in LINKS] >= 0 <= data[i, j, "capacity"];

minimize Total_Cost: sum {<i, j> in LINKS } data[i, j, "cost"] * Ship[i, j];

subto Balance: 
   forall {<k> in CITIES }
       supply[k] + sum {<i, k> in LINKS} Ship[i, k] >= demand[k] + sum {<k, j> in LINKS} Ship[k,j]; # The supply at each site meets the demand.


print "------------- Solving using Optimization Solver---------------";
option solver mindopt; # (Optional) Specifies the solver used for solving the problem. Optimization Solver is used by default.
#option mindopt_options 'print=0'; # Sets output levels for the solver to simplify outputs.
solve; # Solves the problem.

print "-----------------Display---------------";
display; # Displays the result.
print "The lowest shipping cost after optimization = " , sum {<i, j> in LINKS } data[i, j, "cost"] * Ship[i, j];

    Result and result usage

    The logs vary based on code. The following section provides a part of the logs.

    ...
Model summary.
 - Num. variables     : 9
 - Num. constraints   : 5
 - Num. nonzeros      : 15
 - Bound range        : [5.0e+01,4.5e+02]
 - Objective range    : [1.3e+00,3.5e+00]
 - Matrix range       : [1.0e+00,1.0e+00]
...
Simplex method terminated. Time : 0.008s


OPTIMAL; objective 2123.00
...
----------------- Result ---------------
The lowest shipping cost after optimization = 2123

    The optimal solution is 2123. To view more details, such as decision variable values or to verify constraints, you can use the `print` command. You can also retrieve variable values from the .sol file that is created by the program. Alternatively, you can call the display command to retrieve the values of all variables.

    For example, run the following command to verify the constraint that the sum of the goods available at a site plus the goods shipped into that site is equal to the sum of the goods needed at that site plus the goods shipped out of that site.

    forall {<k> in CITIES } 
 print 'The sum of products supplied by site {} and products shipped into it is {}'%k ,
 supply[k] + sum {<i, k> in LINKS} Ship[i, k];
print "-------------------";    
forall {<k> in CITIES } 
 print 'The sum of products needed by site {} and products shipped out of it is {}'%k ,
 demand[k] + sum {<k, j> in LINKS} Ship[k,j];

    Results:

    The sum of products supplied by site HN and products shipped into it is 450
The sum of products supplied by site NE and products shipped into it is 250
The sum of products supplied by site SE and products shipped into it is 200
The sum of products supplied by site LN and products shipped into it is 120
The sum of products supplied by site JL and products shipped into it is 120
The sum of products supplied by site HLJ and products shipped into it is 50
The sum of products supplied by site JS and products shipped into it is 90
The sum of products supplied by site ZJ and products shipped into it is 70
-------------------
The sum of products needed by site HN and products shipped out of it is 450
The sum of products needed by site NE and products shipped out of it is 250
The sum of products needed by site SE and products shipped out of it is 200
The sum of products needed by site LN and products shipped out of it is 120
The sum of products needed by site JL and products shipped out of it is 120
The sum of products needed by site HLJ and products shipped out of it is 50
The sum of products needed by site JS and products shipped out of it is 90
The sum of products needed by site ZJ and products shipped out of it is 70

    Run the following code to display the results in CSV format as a solution to the transportation problem in logistics services:

    print "{},{},{} "% "Start site","Intermediate site","Quantity of goods" : "Results.csv";
close "Results.csv";

forall {<i, j> in LINKS}
    print "{},{},{}" % i,j,Ship[i,j]  >> "Results.csv";

close "Results.csv";

    The following result is returned:

    image.png

    The results indicate that the lowest cost for shipping goods from the factory to each warehouse is 2123. The following shipping scheme is recommended:

    • The amount of goods shipped from the factory HN to the distribution center NE is 250 and to the distribution center SE is 200.

      • From the NE distribution center, ship 100 units to the LN warehouse, 100 units to the JL warehouse, and 50 units to the HLJ warehouse.

      • The amount of goods shipped from the distribution center SE to the warehouse LN is 20, to the warehouse JL is 20, to the warehouse JS is 90, and to the warehouse ZJ is 70.

        • This results in the following totals at the warehouses: 120 units at LN, 120 at JL, 50 at HLJ, 90 at JS, and 70 at ZJ.

          • The total transportation cost from the two distribution centers to the repositories is 2123.

    image.png