PostgreSQL Best Practices: Supporting 25.1 Billion Parcels Per Day

This article discusses the architecture and performance of spatial data management in the Cainiao terminal tracking system that uses plane-plane judgment.

By Digoal

Background

An essential requirement in the Cainiao terminal tracking project is plane-plane judgment.

The database stores tens of millions of polygon records. Each polygon represents a region, for example, a residential area, on a map.

Different express companies use different polygon division methods in order to assign regions (polygons) to each branch and each courier.

When a user needs to send a parcel, the owner branch or courier of the user's region is queried based on the user's location.

1) Requirements

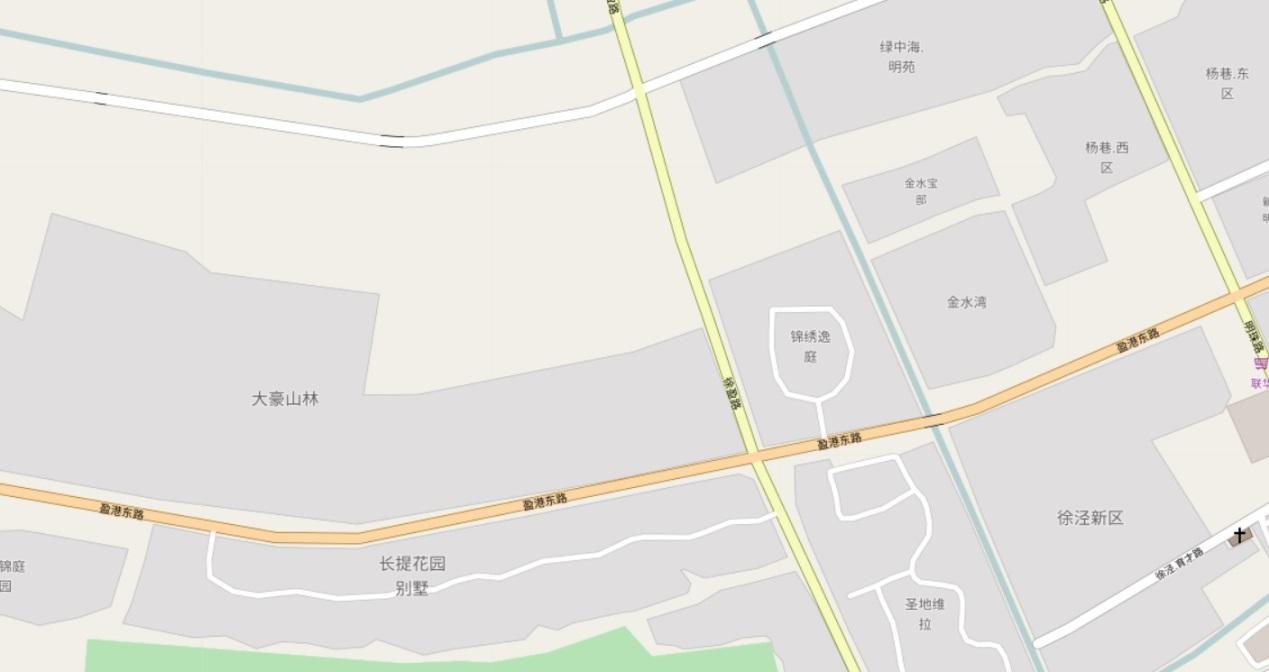
1) The database stores some static plane information that represents residential areas, parks, office buildings, etc. No planes intersect with each other.

2) To support different business types, a map may be divided into different polygons.

For example, different express companies use different polygon division methods in order to assign regions (polygons) to each branch and each courier.

Therefore, a map has multiple layers, each of which may use a different polygon division method.

3) During parcel delivery or pickup, the polygon covering the express company's or user's location is calculated based on the express company's or the user's location. In other words, this region's owner branch or courier is quickly found.

2) Architecture Design

ApsaraDB RDS for PostgreSQL and the PostGIS extension provided by PostgreSQL are used.

The following two PostGIS functions are used: http://postgis.net/docs/manual-2.3/ST_Within.html

2.1) ST_within

Let's recap the concepts of ST_within as described by this page.

ST_Within - Returns true if geometry A is completely inside geometry B

boolean ST_Within(geometry A, geometry B);

Returns TRUE if geometry A is entirely inside geometry B. For this function to make sense, the source geometries must both be of the same coordinate projection, having the same SRID. If ST_Within(A,B) is true and ST_Within(B,A) is true, then the two geometries are considered spatially equal.

This function call automatically includes a bounding box comparison that uses any indexes available on the geometries. To avoid index use, use the function _ST_Within.

-- a circle within a circle      
SELECT ST_Within(smallc,smallc) As smallinsmall,      
        ST_Within(smallc, bigc) As smallinbig,      
        ST_Within(bigc,smallc) As biginsmall,      
        ST_Within(ST_Union(smallc, bigc), bigc) as unioninbig,      
        ST_Within(bigc, ST_Union(smallc, bigc)) as biginunion,      
        ST_Equals(bigc, ST_Union(smallc, bigc)) as bigisunion      
FROM      
(      
SELECT ST_Buffer(ST_GeomFromText('POINT(50 50)'), 20) As smallc,      
        ST_Buffer(ST_GeomFromText('POINT(50 50)'), 40) As bigc) As foo;      
-- Result      
 smallinsmall | smallinbig | biginsmall | unioninbig | biginunion | bigisunion      
--------------+------------+------------+------------+------------+------------      
 t            | t          | f          | t          | t          | t      
(1 row)

2.2) ST_Contains

Let's recap the concepts of ST_within as described by this page.

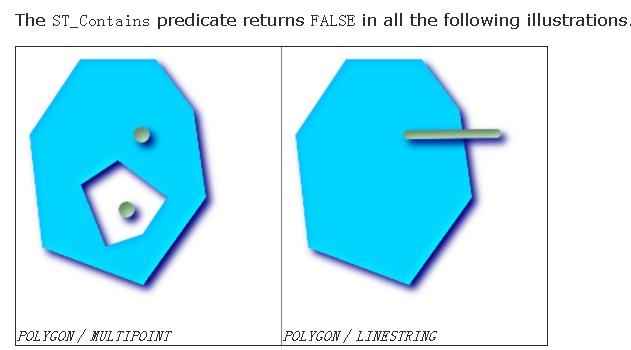
ST_Contains - Returns true if and only if no points of B lie in the exterior of A, and at least one point of the interior of B lies in the interior of A.

boolean ST_Contains(geometry geomA, geometry geomB);

Returns TRUE if geometry B is entirely inside geometry A. For this function to make sense, the source geometries must both be of the same coordinate projection, having the same SRID. ST_Contains is the inverse of ST_Within. So, ST_Contains(A,B) implies ST_Within(B,A) except in the case of invalid geometries where the result is always false regardless or not defined.

This function call automatically includes a bounding box comparison that uses any indexes available on the geometries. To avoid index use, use the function _ST_Contains.

-- A circle within a circle      
SELECT ST_Contains(smallc, bigc) As smallcontainsbig,      
           ST_Contains(bigc,smallc) As bigcontainssmall,      
           ST_Contains(bigc, ST_Union(smallc, bigc)) as bigcontainsunion,      
           ST_Equals(bigc, ST_Union(smallc, bigc)) as bigisunion,      
           ST_Covers(bigc, ST_ExteriorRing(bigc)) As bigcoversexterior,      
           ST_Contains(bigc, ST_ExteriorRing(bigc)) As bigcontainsexterior      
FROM (SELECT ST_Buffer(ST_GeomFromText('POINT(1 2)'), 10) As smallc,      
                         ST_Buffer(ST_GeomFromText('POINT(1 2)'), 20) As bigc) As foo;      
      
-- Result      
  smallcontainsbig | bigcontainssmall | bigcontainsunion | bigisunion | bigcoversexterior | bigcontainsexterior      
------------------+------------------+------------------+------------+-------------------+---------------------      
 f                | t                | t                | t          | t        | f      
      
-- Example demonstrating difference between contains and contains properly      
SELECT ST_GeometryType(geomA) As geomtype, ST_Contains(geomA,geomA) AS acontainsa, ST_ContainsProperly(geomA, geomA) AS acontainspropa,      
   ST_Contains(geomA, ST_Boundary(geomA)) As acontainsba, ST_ContainsProperly(geomA, ST_Boundary(geomA)) As acontainspropba      
FROM (VALUES ( ST_Buffer(ST_Point(1,1), 5,1) ),      
                         ( ST_MakeLine(ST_Point(1,1), ST_Point(-1,-1) ) ),      
                         ( ST_Point(1,1) )      
          ) As foo(geomA);      
      
  geomtype    | acontainsa | acontainspropa | acontainsba | acontainspropba      
--------------+------------+----------------+-------------+-----------------      
ST_Polygon    | t          | f              | f           | f      
ST_LineString | t          | f              | f           | f      
ST_Point      | t          | t              | f           | f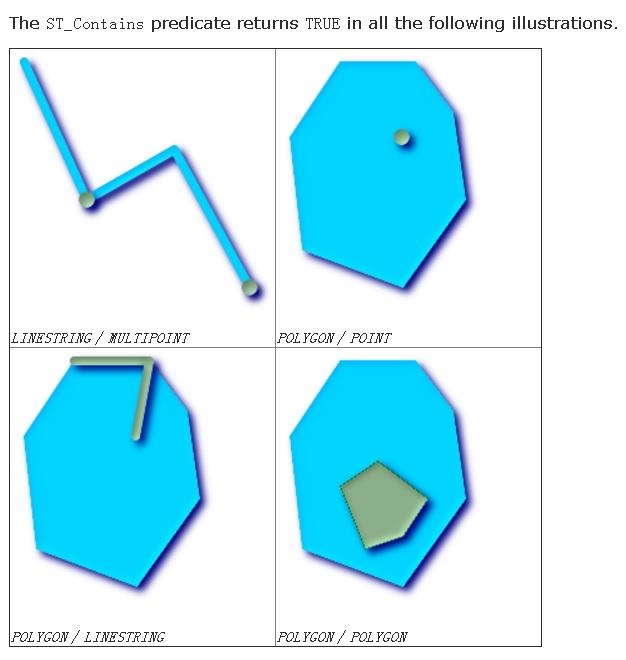

3) Demo and Performance

3.1) Stress Test Plane-point Search Using Built-in PostgreSQL Geometric Data Types

To simplify the test, we use the built-in geometric data types provided by PostgreSQL during the test. The usage of these data types is similar to that of PostGIS data types.

3.1.1) Create a Test Table

postgres=# create table po(id int, typid int, po polygon);    
CREATE TABLE

3.1.2) Create a Partition Table or a Partition Index

create extension btree_gist;    
create index idx_po_1 on po using gist(typid, po);

3.1.3) Optional: Create a Spatial Exclusion Constraint

If required, create spatial exclusion constraints to prevent polygons with a specific typid from overlapping.

Note: && means that TRUE is returned when the polygons' bounding boxes intersect with each other. As a result, two polygons that do not intersect with each other but whose bounding boxes intersect with each other may not be included.

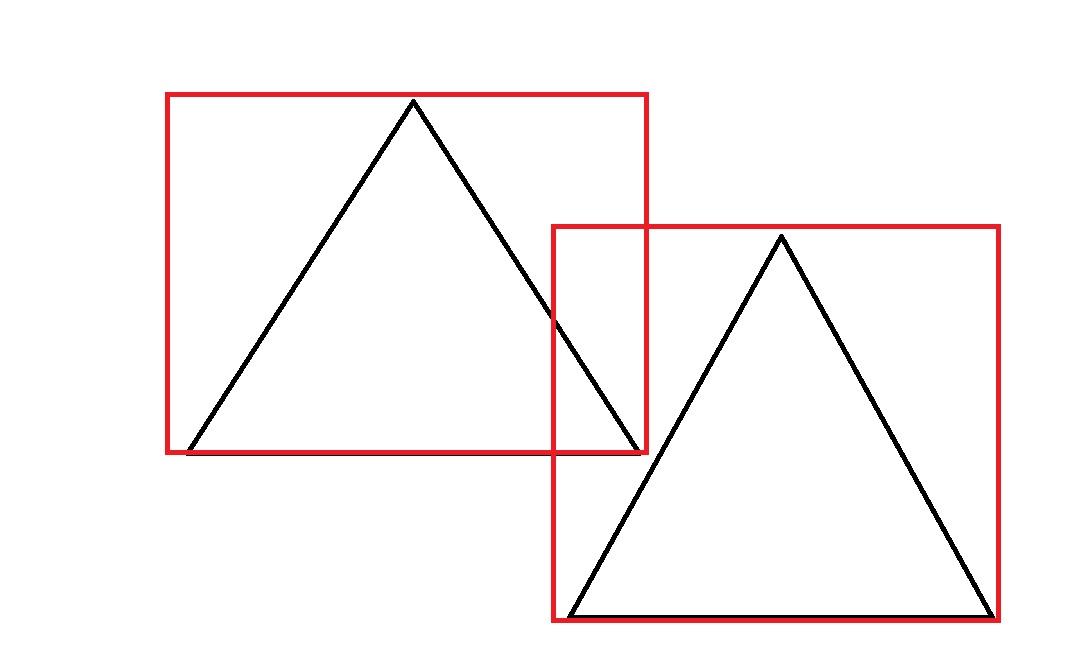
To resolve this problem, use the function-based data write method described below in this article instead of the INSERT method or the exclusion constraint.

create table tbl_po(id int, typid int, po polygon)    
PARTITION BY LIST (typid);    
    
CREATE TABLE tbl_po_1    
    PARTITION OF tbl_po (    
    EXCLUDE USING gist (po WITH &&)    
) FOR VALUES IN (1);    
    
...    
    
CREATE TABLE tbl_po_20    
    PARTITION OF tbl_po (    
    EXCLUDE USING gist (po WITH &&)    
) FOR VALUES IN (20);    
    
查看某分区表的空间排他约束如下    
    
postgres=# \d tbl_po_1    
             Table "postgres.tbl_po_1"    
 Column |  Type   | Collation | Nullable | Default     
--------+---------+-----------+----------+---------    
 id     | integer |           |          |     
 typid  | integer |           |          |     
 po     | polygon |           |          |     
Partition of: tbl_po FOR VALUES IN (1)    
Indexes:    
    "tbl_po_1_po_excl" EXCLUDE USING gist (po WITH &&)

3.1.4) Write 10 Million Polygon Records as Test Data

insert into po select id, random()*20, polygon('(('||x1||','||y1||'),('||x2||','||y2||'),('||x3||','||y3||'))') from (select id, 180-random()*180 x1, 180-random()*180 x2, 180-random()*180 x3, 90-random()*90 y1, 90-random()*90 y2, 90-random()*90 y3 from generate_series(1,10000000) t(id)) t;

3.1.5) Test the Plane-Point Judgment Performance

Query the polygon containing the point(1,1), where the response time is 0.57 milliseconds.

postgres=# explain (analyze,verbose,timing,costs,buffers) select * from po where typid=1 and po @> polygon('((1,1),(1,1),(1,1))') limit 1;    
                                                           QUERY PLAN                                                              
---------------------------------------------------------------------------------------------------------------------------------  
 Limit  (cost=0.42..1.76 rows=1 width=93) (actual time=0.551..0.551 rows=1 loops=1)  
   Output: id, typid, po  
   Buffers: shared hit=74  
   ->  Index Scan using idx_po_1 on postgres.po  (cost=0.42..673.48 rows=503 width=93) (actual time=0.550..0.550 rows=1 loops=1)  
         Output: id, typid, po  
         Index Cond: ((po.typid = 1) AND (po.po @> '((1,1),(1,1),(1,1))'::polygon))  
         Rows Removed by Index Recheck: 17  
         Buffers: shared hit=74  
 Planning time: 0.090 ms  
 Execution time: 0.572 ms  
(10 rows)

3.1.6) Conduct a Stress Test

vi test.sql    
\set x random(-180,180)  
\set y random(-90,90)  
\set typid random(1,20)  
select * from po where typid=:typid and po @> polygon('((:x,:y),(:x,:y),(:x,:y))') limit 1;   
    
pgbench -M simple -n -r -P 1 -f ./test.sql -c 64 -j 64 -T 100    
transaction type: ./test.sql  
scaling factor: 1  
query mode: simple  
number of clients: 64  
number of threads: 64  
duration: 100 s  
number of transactions actually processed: 29150531  
latency average = 0.220 ms  
latency stddev = 0.140 ms  
tps = 291487.813205 (including connections establishing)  
tps = 291528.228634 (excluding connections establishing)  
script statistics:  
 - statement latencies in milliseconds:  
         0.002  \set x random(-180,180)  
         0.001  \set y random(-90,90)  
         0.000  \set typid random(1,20)  
         0.223  select * from po where typid=:typid and po @> polygon('((:x,:y),(:x,:y),(:x,:y))') limit 1;

What a success! 290,000 TPS; average response time: 0.2 milliseconds.

3.2) Stress Test Plane-Point Search in the PostGIS Spatial Database

ApsaraDB RDS for PostgreSQL and AnalyticDB for PostgreSQL come with the built-in spatial database extension PostGIS. Create a PostGIS extension before using them.

create extension postgis;

3.2.1) Create a Table

postgres=# create table po(id int, typid int, po geometry);    
CREATE TABLE

3.2.2) Create a Spatial Index

postgres=# create extension btree_gist;    
postgres=# create index idx_po_1 on po using gist(typid, po);

3.2.3) Write 10 Million Polygon Records as Test Data

postgres=# insert into po   
select   
  id, random()*20,   
  ST_PolygonFromText('POLYGON(('||x1||' '||y1||','||x2||' '||y2||','||x3||' '||y3||','||x1||' '||y1||'))')   
from   
(  
  select id, 180-random()*180 x1, 180-random()*180 x2, 180-random()*180 x3, 90-random()*90 y1, 90-random()*90 y2, 90-random()*90 y3 from generate_series(1,10000000) t(id)  
) t;

3.2.4) Test the Plane-point Judgment Performance

postgres=# explain (analyze,verbose,timing,costs,buffers) select * from po where typid=1 and st_within(ST_PointFromText('POINT(1 1)'), po) limit 1;    
                                                         QUERY PLAN                                                            
-----------------------------------------------------------------------------------------------------------------------------  
 Limit  (cost=0.42..4.21 rows=1 width=40) (actual time=0.365..0.366 rows=1 loops=1)  
   Output: id, typid, po  
   Buffers: shared hit=14  
   ->  Index Scan using idx_po_1 on public.po  (cost=0.42..64.92 rows=17 width=40) (actual time=0.364..0.364 rows=1 loops=1)  
         Output: id, typid, po  
         Index Cond: ((po.typid = 1) AND (po.po ~ '0101000000000000000000F03F000000000000F03F'::geometry))  
         Filter: _st_contains(po.po, '0101000000000000000000F03F000000000000F03F'::geometry)  
         Rows Removed by Filter: 1  
         Buffers: shared hit=14  
 Planning time: 0.201 ms  
 Execution time: 0.389 ms  
(11 rows)  

postgres=# select id,typid,st_astext(po) from po where typid=1 and st_within(ST_PointFromText('POINT(1 1)'), po) limit 5;  
   id    | typid |                                                                       st_astext                                                                        
---------+-------+--------------------------------------------------------------------------------------------------------------------------------------------------------
 9781228 |     1 | POLYGON((0.295946141704917 0.155529817566276,16.4715472329408 56.1022255802527,172.374844718724 15.4784881789237,0.295946141704917 0.155529817566276))
  704428 |     1 | POLYGON((173.849076312035 77.8871315997094,167.085936572403 23.9897218951955,0.514283403754234 0.844541620463133,173.849076312035 77.8871315997094))
 5881120 |     1 | POLYGON((104.326644698158 44.4173073163256,3.76680867746472 76.8664212757722,0.798425730317831 0.138536808080971,104.326644698158 44.4173073163256))
 1940693 |     1 | POLYGON((0.774057107046247 0.253543308936059,126.49553722702 22.7823389600962,8.62134614959359 56.176855028607,0.774057107046247 0.253543308936059))
 3026739 |     1 | POLYGON((0.266327261924744 0.406031627207994,101.713274326175 38.6256391229108,2.88589236326516 15.3229149011895,0.266327261924744 0.406031627207994))
(5 rows)

3.2.5) Conduct a Stress Test

vi test.sql  
\setrandom x -180 180  
\setrandom y -90 90  
\setrandom typid 1 20  
select * from po where typid=:typid and st_within(ST_PointFromText('POINT(:x :y)'), po) limit 1;    
  
pgbench -M simple -n -r -P 1 -f ./test.sql -c 64 -j 64 -T 120  
transaction type: Custom query  
scaling factor: 1  
query mode: simple  
number of clients: 64  
number of threads: 64  
duration: 120 s  
number of transactions actually processed: 23779817  
latency average: 0.321 ms  
latency stddev: 0.255 ms  
tps = 198145.452614 (including connections establishing)  
tps = 198160.891580 (excluding connections establishing)  
statement latencies in milliseconds:  
        0.002615        \setrandom x -180 180  
        0.000802        \setrandom y -90 90  
        0.000649        \setrandom typid 1 20  
        0.316816        select * from po where typid=:typid and st_within(ST_PointFromText('POINT(:x :y)'), po) limit 1;

What a success! 198,000 TPS; average response time: 0.32 milliseconds.

4) Technical Points

4.1) Spatial Exclusion Constraint

This constraint can prevent polygons' bounding boxes in a record from intersecting with each other. For example, rigorous data such as maps definitely cannot have overlapping polygons; otherwise, territorial disputes may arise.

Do not be surprised. PostgreSQL can be this rigorous.

-- 例子

CREATE TABLE tbl_po_1    
    PARTITION OF tbl_po (    
    EXCLUDE USING gist (po WITH &&)    
) FOR VALUES IN (1);

Note: && means that TRUE is returned when the polygons' bounding boxes intersect with each other. As a result, two objects that do not intersect with each other but whose bounding boxes intersect with each other cannot be included.

To resolve this problem, use the function-based data write method and use pg_try_advisory_xact_lock and ST_Intersects to ensure constraint consistency, thereby preventing constraints unreliability caused by concurrent write operations.

postgres=# select ST_Intersects(st_makepolygon(ST_LineFromText('LINESTRING(1 1,2 1,1.5 2,1 1)') ), st_makepolygon(ST_LineFromText('LINESTRING(1.9 1.9,3 1.9,2.5 3,1.9 1.9)') ));
 st_intersects 
---------------
 f
(1 row)

postgres=# select st_makepolygon(ST_LineFromText('LINESTRING(1 1,2 1,1.5 2,1 1)') ) && st_makepolygon(ST_LineFromText('LINESTRING(1.9 1.9,3 1.9,2.5 3,1.9 1.9)') );
 ?column? 
----------
 t
(1 row)


create table tbl(id int, geo geometry);
create index idx_tbl_1 on tbl using gist (geo);

create or replace function insert_tbl (int, geometry) returns void as $$
declare
  vid int;
  var geometry;
begin
  loop
    if pg_try_advisory_xact_lock(1) then -- 串行写
      select geo into var from tbl where ST_Intersects(geo, $2) limit 1;
      if not found then
        insert into tbl (id, geo) values ($1, $2);
return;
      else
        raise notice '% intersect with %,%, this row not inserted.', $2, vid,var;
return;
      end if;
    end if;
  end loop;
end;
$$ language plpgsql strict;

postgres=# select insert_tbl(1,st_makepolygon(ST_LineFromText('LINESTRING(1 1,2 1,1.5 2,1 1)') ));
 insert_tbl 
------------
 
(1 row)

postgres=# select insert_tbl(1,st_makepolygon(ST_LineFromText('LINESTRING(1 1,2 1,1.5 2,1 1)') ));
NOTICE:  01030000000100000004000000000000000000F03F000000000000F03F0000000000000040000000000000F03F000000000000F83F0000000000000040000000000000F03F000000000000F03F intersect with <NULL>,01030000000100000004000000000000000000F03F000000000000F03F0000000000000040000000000000F03F000000000000F83F0000000000000040000000000000F03F000000000000F03F, this row not inserted.
 insert_tbl 
------------
 
(1 row)

postgres=# select insert_tbl(1,st_makepolygon(ST_LineFromText('LINESTRING(1.9 1.9,3 1.9,2.5 3,1.9 1.9)') ));
 insert_tbl 
------------
 
(1 row)

http://postgis.net/docs/manual-2.5/ST_Intersects.html

4.2) Partition Tables

In the example described in this article, different express companies correspond to different layers. Each express company divides an area into multiple polygons based on the regions (polygons) assigned to branches and couriers.

Use LIST partitioning to make each partition correspond to one express company.

4.3) Spatial Indexes

The GiST spatial index supports various spatial search manners, including KNN, inclusion, intersection, and up, down, left, right (UDLR). It is highly efficient.

4.4) Plane-plane and Plane-point Judgment

Plane-plane judgment and plane-point judgment are the main requirements in the example described in this article. When a user needs to send a parcel, a polygon covering the user's location is selected from over 10 million polygons in the database based on the user's location.

5) Cloud Products

ApsaraDB RDS for PostgreSQL

6) Summary

With ApsaraDB RDS for PostgreSQL, a database can store approximately 10 million polygons. A single database's processing rate can reach 290,000 TPS, and the average response time of a single request is about 0.2 milliseconds.

7) References

http://postgis.net/docs/manual-2.3/ST_Within.html

Community