Migrating Oracle PL/SQL Applications to AnalyticDB for PostgreSQL

By Lu Feng.

AnalyticDB for PostgreSQL is compatible with Oracle syntax, and therefore you can easily migrate oracle applications to AnalyticDB for PostgreSQL. In this blog, you will learn how you can specifically migrate Oracle PL/SQL applications to AnalyticDB for PostgreSQL. This blog can also be a good point reference when you need to do various migration operations.

The Open-source Ora2Pg Tool

Before starting to convert Oracle Procedural Language (PL), you can use the open-source tool Ora2Pg to implement preliminary conversion. You can also use Ora2Pg to convert DDL, view, and packages in Oracle to [PostgreSQL-compatible syntax. However, you may need to manually correct converted SQL scripts because the PostgreSQL syntax version after scripts are converted is often of a later version than the PostegreSQL kernel version used by AnalyticDB for PostgreSQL and rules that Ora2Pg depends on for conversion may be missing or incorrect. For this, generally the best thing to do is to run converted SQL scripts on ADB for PG first to see whether syntax errors or unexpected results are reported, and then, after this, you can manually make corrections.

Data Type Conversion Table

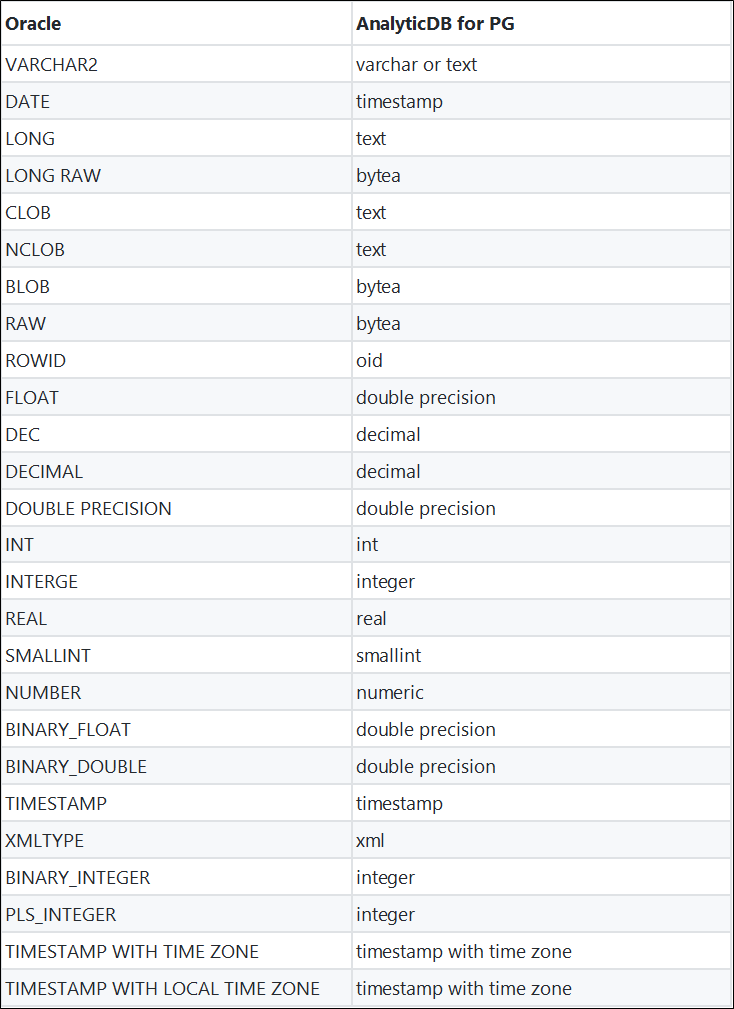
Below is a conversion comparison of Oracle and AnalyticDB for PostgreSQL data types.

System Function Conversion Table

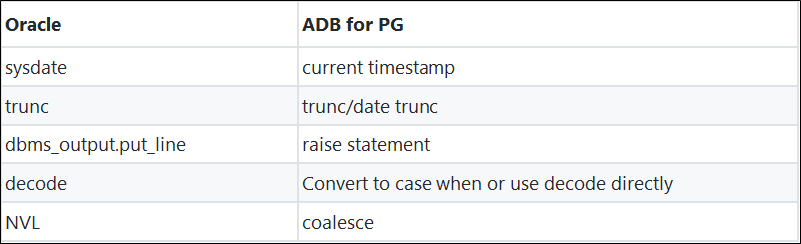
Below is a comparison of Oracle and AnalyticDB for PostgreSQL system functions.

PL/SQL and PL/pgSQL

PL/SQL, which stands for Procedural Language/SQL, is a procedural SQL language extension. It is an extension of SQL statements implemented by Oracle and allows SQL to have some programming language features. Therefore, PL/SQL can be used to implement complex business logic. PL/SQL is equivalent to PL/pgSQL, which stands for Procedural Language/PostgreSQL, in AnalyticDB for PostgreSQL.

Package

PL/pgSQL (Procedural Language/PostgreSQL) in AnalyticDB for PostgreSQL does not support packages. As a result, packages need to be converted to schemas, and all the procedures and functions in packages need to be converted functions in AnalyticDB for PostgreSQL.

For example, consider the following. You'll want to convert the following:

create or replace package pkg is 
…
end;

To this code below:

create schema pkg;

1. Variables defined in the package:

 procedure/function The local variables remain unchanged, and global variables can be saved in ADB for PG using temporary tables. See section 1.4.5 for more information.block for the package

2. The initialization block for the package:

If you can delete it, delete it, if you can't delete it, you can use function wrapper and call the function actively when needed.

3. The procedure/function defined in the package:

4. The procedure and function defined in the package are converted into the function of adb for pg, and the function is defined into the schema corresponding to the package.

For example, there is a package named pkg with the following functions:

FUNCTION test_func (args int) RETURN int is 
var number := 10;
BEGIN
… … 
END;
Converted to the function of ADB for PG：
CREATE OR REPLACE FUNCTION pkg. test_func(args int) RETURNS int AS 

$$


  … …  


$$

 LANGUAGE plpgsql;

Procedure/Function

Convert Oracle procedures and functions either in the package or globally to functions in AnalyticDB for PostgreSQL.

For example, convert the following:

CREATE OR REPLACE FUNCTION test_func (v_name varchar2, v_version varchar2)
RETURN varchar2 IS
    ret varchar(32);
BEGIN
    IF v_version IS NULL THEN
        ret := v_name;
ELSE
    ret := v_name || '/' || v_version;
    END IF;
    RETURN ret;
END;

To this code below:

CREATE OR REPLACE FUNCTION test_func (v_name varchar, v_version varchar)
RETURNS varchar AS 

$$


DECLARE
    ret varchar(32);
BEGIN
    IF v_version IS NULL THEN
        ret := v_name;
ELSE
    ret := v_name || '/' || v_version;
    END IF;
    RETURN ret;
END;


$$

 LANGUAGE plpgsql;

Some key points to take consideration of when in procedure/function conversions:

The RETURN keyword is converted to RETURNS.
Use &dollar;\$ ... &dollar;\$ to package a function body.
You should pay special attention to function language declarations.
A subprocedure also needs to be converted to a function in AnalyticDB for PostgreSQL.

PL Statement

For Statement

The FOR loop with REVERSE statements work differently: The reversion order in PL/SQL is from the second number to the first number, whereas in PL/pgSQL the order is from the first number to the second number. So, what does that mean anyway? Well, in the conversion process, when the FOR loop is ported, the loop boundaries must be exchanged.

To make it clearer, consider the following example. You'll want to convert the following:

FOR i IN REVERSE 1..3 LOOP
    DBMS_OUTPUT.PUT_LINE (TO_CHAR(i));
END LOOP;

To the following code:

FOR i IN REVERSE 3..1 LOOP
    RAISE '%' ,i;
END LOOP;

PRAGMA Statement

PRAGMA statements do not exist in AnalyticDB for PostgreSQL, and therefore they need to be deleted.

Transaction Processing

Transactional control statements such as begin, commit, and rollback cannot be used within functions in AnalyticDB for PostgreSQL.

Modification method:

Delete transactional control statements in the function body and put them outside the function body.
Split the function into several functions based on commit/rollback.

EXECUTE Statement

AnalyticDB for PostgreSQL supports dynamic SQL statements that are similar to statements in Oracle. However, AnalyticDB for PostgreSQL differs from Oracle in the following aspects:

The using syntax is not supported. The corresponding solution is to join parameters into SQL strings.
Use quote_ident to package database identifiers and quote_literal to package values.

For example, convert the following:

EXECUTE 'UPDATE employees_temp SET commission_pct = :x' USING a_null;

To this code below:

EXECUTE 'UPDATE employees_temp SET commission_pct = ' || quote_literal(a_null);

Pipe Row

Use table functions in AnalyticDB for PostgreSQL to replace Pipe Row functions.

For example, convert the following:

TYPE pair IS RECORD(a int, b int);
TYPE numset_t IS TABLE OF pair;

FUNCTION f1(x int) RETURN numset_t PIPELINED IS
DECLARE
    v_p pair;
BEGIN
    FOR i IN 1..x LOOP
      v_p.a := i;
      v_p.b := i+10;
      PIPE ROW(v_p);
    END LOOP;
    RETURN;
END;

select * from f1(10);

To this code below:

create type pair as (a int, b int);

create or replace function f1(x int) returns setof pair as 

$$


declare
rec pair;
begin
    for i in 1..x loop
        rec := row(i, i+10);
        return next rec;
    end loop;
    return ;
end


$$

 language 'plpgsql';

select * from f1(10);

1. Convert the custom type pair to the composite type pair.
2. The Table Of type does not need to be defined. Replace it with Set Of in AnalyticDB for PostgreSQL.
3. The Pipe Row statement is converted to the two following statements:

  rec := row(i);
  return next rec;

4. The preceding Oracle function can also be converted to:

create or replace function f1(x int) returns setof record as 

$$

    
declare
rec record;
begin
    for i in 1..x loop
        rec := row(i, i+10);
        return next rec;
    end loop;
    return ;
end
    

$$

language 'plpgsql';

The difference from the first option is that the data type numset_t is not required to be pre-defined. This is exactly why a return type needs to be specified when a query is performed, for example, by using select * from f1(10) as (a int, b int);.

Exception Handling

Use Raise to throw an exception.
After the exception is caught, the transaction cannot be rolled back internally. Rollback is only allowed outside user-defined functions.
For error codes supported in AnalyticDB for PostgreSQL, see this page.

When Both Return and Out Parameters Are Included in a Function

In AnalyticDB for PostgreSQL, a function cannot contain the Return parameter and the Out parameter at the same time. Therefore, the parameter to be returned needs to be rewritten as an Out parameter.

For example, convert the following:

CREATE OR REPLACE FUNCTION test_func(id int, name varchar(10), out_id out int) returns varchar(10)
AS $body$
BEGIN
      out_id := id + 1;
      return name;
end
$body$
LANGUAGE PLPGSQL;

To this code below:

CREATE OR REPLACE FUNCTION test_func(id int, name varchar(10), out_id out int, out_name out varchar(10))
AS $body$
BEGIN
      out_id := id + 1;
      out_name := name;
end
$body$
LANGUAGE PLPGSQL;

Then run select * from test_func(1,'1') into rec; to obtain the return value of the corresponding field from rec.

When a Variable in a String Connection Contains an Apostrophe

In the following example, the variable param2 is of string type. Assume that the value of param2 is adb'-'pg. When the following sql_str is directly used in AnalyticDB for PostgreSQL, - will be recognized as an operator, causing an error. The statement must be converted by using the quote_literal function.

For example, convert the following:

sql_str := 'select * from test1 where col1 = ' || param1 || ' and col2 = '''|| param2 || '''and col3 = 3';

To this code below:

sql_str := 'select * from test1 where col1 = ' || param1 || ' and col2 = '|| quote_literal(param2) || 'and col3 = 3';

Obtain the Days between Two Timestamps

To obtain the days between two timestamps, you can do the following conversion:

SELECT to_date('2019-06-30 16:16:16') – to_date('2019-06-29 15:15:15') + 1 INTO v_days from dual;

To this code below:

SELECT extract('days' from '2019-06-30 16:16:16'::timestamp - '2019-06-29 15:15:15'::timestamp + '1 days'::interval)::int INTO v_days;

PL Data Types

Record

For Record, convert it to a composite type in AnalyticDB for PostgreSQL.

For example, convert the following:

TYPE rec IS RECORD (a int, b int)；

To this code below:

CREATE TYPE rec AS (a int, b int);

Nested Table

1. As a variable in PL/SQL, a nested table can be converted to the array type in AnalyticDB for PostgreSQL.

For example, convert the following:

DECLARE
  TYPE Roster IS TABLE OF VARCHAR2(15);
  names Roster := 
  Roster('D Caruso', 'J Hamil', 'D Piro', 'R Singh');
BEGIN
  FOR i IN names.FIRST .. names.LAST
  LOOP
      IF names(i) = 'J Hamil' THEN
        DBMS_OUTPUT.PUT_LINE(names(i));
      END IF;
  END LOOP;
END;

To this code below:

create or replace function f1() returns void as 

$$


declare
    names varchar(15)[] := '{"D Caruso", "J Hamil", "D Piro", "R Singh"}';
    len int := array_length(names, 1);
begin
    for i in 1..len loop
        if names[i] = 'J Hamil' then
            raise notice '%', names[i];
        end if;
    end loop;
    return ;
end


$$

 language 'plpgsql';

select f();

2. When a nested table is used as the return value, replace it with the table function (see Section 1.3.5).

Associative Array

Currently, no conversion type is available for this type.

Variable-Size Arrays

Like with a nested table, for variable-size arrays, simply convert to the array type.

Global Variables

Currently, AnalyticDB for PostgreSQL does not support global variables. One solution is to store all the global variables into one temporary table and define the function to modify and obtain global variables.

For example, consider the following:

create temporary table global_variables (
        id int,
        g_count int,
        g_set_id varchar(50),
        g_err_code varchar(100)
);

insert into global_variables values(0, 1, null，null);

CREATE OR REPLACE FUNCTION get_variable() returns setof global_variables AS


$$


DECLARE
    rec global_variables%rowtype;
BEGIN
    execute 'select * from global_variables' into rec;
    return next rec;
END;


$$

 LANGUAGE plpgsql;

CREATE OR REPLACE FUNCTION set_variable(in param varchar(50), in value anyelement) returns void AS


$$


BEGIN
    execute 'update global_variables set ' ||  quote_ident(param) || ' = ' || quote_literal(value);
END;


$$

 LANGUAGE plpgsql;

The ID field is the distribution column of the temporary table global_variables. Next, because it is not allowed to modify the distribution column in AnalyticDB for PostgreSQL, this field is additionally needed.

tmp_rec record;

To modify a global variable, use:

select * from set_variable('g_error_code', 'error'::varchar) into tmp_rec;

To obtain a global variable, use:

select * from get_variable() into tmp_rec; error_code := tmp_rec.g_error_code;

SQL

Connect By

Connect By is used to process hierarchical queries in Oracle. No equivalent SQL statement can be found in AnalyticDB for PostgreSQL. An conversion option is to use circular iteration by hierarchy.

For example, convert the following:

create table employee(
       emp_id numeric(18),
       lead_id numeric(18),
       emp_name varchar(200),
       salary numeric(10,2),
       dept_no varchar(8)
);
insert into employee values('1',0,'king','1000000.00','001');
insert into employee values('2',1,'jack','50500.00','002');
insert into employee values('3',1,'arise','60000.00','003');
insert into employee values('4',2,'scott','30000.00','002');
insert into employee values('5',2,'tiger','25000.00','002');
insert into employee values('6',3,'wudde','23000.00','003');
insert into employee values('7',3,'joker','21000.00','003');
insert into employee values('3',7,'joker','21000.00','003');
select emp_id,lead_id,emp_name,prior emp_name as lead_name,salary
     from employee
     start with  lead_id=0
     connect by prior emp_id =  lead_id

To this code below:

create or replace function f1(tablename text, lead_id int, nocycle boolean) returns setof employee as 

$$


declare
    idx int := 0;
    res_tbl varchar(265) := 'result_table';
    prev_tbl varchar(265) := 'tmp_prev';
    curr_tbl varchar(256) := 'tmp_curr';

    current_result_sql varchar(4000);
    tbl_count int;

    rec record;
begin
    
    execute 'truncate ' || prev_tbl;
    execute 'truncate ' || curr_tbl;
    execute 'truncate ' || res_tbl;
    loop
        -- Query the current level result and insert it into the tmp_curr table
        current_result_sql := 'insert into ' || curr_tbl || ' select t1.* from ' || tablename || ' t1';

        if idx > 0 then
            current_result_sql := current_result_sql || ', ' || prev_tbl || ' t2 where t1.lead_id = t2.emp_id';
        else
            current_result_sql := current_result_sql || ' where t1.lead_id = ' || lead_id;
        end if;
        execute current_result_sql;

        -- If there is a ring, delete the data that has been traversed
        if nocycle is false then
            execute 'delete from ' || curr_tbl || ' where (lead_id, emp_id) in (select lead_id, emp_id from ' || res_tbl || ') ';
        end if;

        -- Exit if there is no data
        execute 'select count(*) from ' || curr_tbl into tbl_count;
        exit when tbl_count = 0;

        -- Save the tmp_curr data to the result table
        execute 'insert into ' || res_tbl || ' select * from ' || curr_tbl;
        execute 'truncate ' || prev_tbl;
        execute 'insert into ' || prev_tbl || ' select * from ' || curr_tbl;
        execute 'truncate ' || curr_tbl;
        idx := idx + 1;
    end loop;

    -- Return result
    current_result_sql := 'select * from ' || res_tbl;
    for rec in execute current_result_sql loop
        return next rec;
    end loop;
    return;
end


$$

 language plpgsql;

Rownum

1. This is used to limit the size of a result set. This can be replaced by limit.

For example, convert the following:

select * from t where rownum < 10;

To the code below:

select * from t limit 10;

2. Use row_number() over() to generate rownum.

For example, convert the following:

select rownum, * from t;

To the code below:

select row_number() over() as rownum, * from t;

DUAL Table

1. Remove DUAL.

For example, convert the following:

select sysdate from dual;

To this code below:

select current_timestamp;

2. Create a DUAL table.

User-Defined Functions in `SELECT`

AnalyticDB for PostgreSQL supports invoking user-defined functions in SELECT. However, user-defined functions cannot contain SQL statements. Otherwise the following error will occur:

ERROR: function cannot execute on segment because it accesses relation "public.t2" (functions.c:155) (seg1 slice1 127.0.0.1:25433 pid=52153) (cdbdisp.c:1326)DETAIL:SQL statement "select b from t2 where a = $1 "

To solve this problem, convert the user-defined functions in SELECT to SQL expressions or subqueries.

For example, convert the following:

create or replace FUNCTION f1(arg int) RETURN int IS
    v int;
BEGIN
    select b into v from t2 where a = arg;
    return v;
END;

select a, f1(b) from t1;

To this code below:

select t1.a, t2.b from t1, t2 where t1.b = t2.a;

(+) Multi-table Outer Join

AnalyticDB for PostgreSQL does not support (+) syntax format. To achieve the same effect, convert this syntax to standard Outer Join syntax.

For example, convert the following:

oracle
select * from a,b where a.id=b.id(+)

To this code below:

select * from a left join b on a.id=b.id

If the (+) syntax involves joining three tables, use wte to join two tables first, and then perform outer join on the wte table and the table connected with +.

For example, convert the following:

Select * from test1 t1, test2 t2, test3 t3 where t1.col1(+) between NVL(t2.col1, t3.col1) and NVL(t3.col1, t2.col1);

To the code below:

with cte as (select t2.col1 as low, t2.col2, t3.col1 as high, t3.col2 as c2 from t2, t3)
select * from t1 right outer join cte on t1.col1 between coalesce(cte.low, cte.high) and coalesce(cte.high,cte.low);

Merge Into

To convert Merge Into syntax, use Update in AnalyticDB for PostgreSQL first, and then use the GET DIAGNOSTICS rowcount := ROW_COUNT; statement to obtain the number of updated rows. If the number of updated rows is 0, use Insert statement to insert data.

MERGE INTO test1 t1
            USING (SELECT t2.col1 col1, t3.col2 col2,
                     FROM test2 t2, test3 t3) S
            ON S.col1 = 1 and S.col2 = 2            
WHEN MATCHED THEN
              UPDATE
              SET test1.col1 = S.col1+1,
                     test1.col2 = S.col2+2
WHEN NOT MATCHED THEN
              INSERT (col1, col2)
              VALUES
                (S.col1+1, S.col2+2);

The preceding is converted to following:

Update test1 t1 SET t1.col1 = test2.col1+1, test3.col2 = S.col2+2 where test2.col1 = 1 and test2.col2 = 2;
GET DIAGNOSTICS rowcount := ROW_COUNT;
if rowcount = 0 then
    insert into test1 values(test2.col1+1, test3.col2+2);
end if;

Sequence

For example, convert the following:

create sequence seq1; 
select seq1.nextval from dual;

To this code below:

create SEQUENCE seq1;
select nextval('seq1');

Cursor

In Oracle, the following statement can be used to iterate through cursors.

For example, convert the following:

FUNCTION test_func() IS
    Cursor data_cursor IS SELECT * from test1;
BEGIN
    FOR I IN data_cursor LOOP
        Do something with I;
END LOOP;
END;

To this code below:

CREATE OR REPLACE FUNCTION test_func()
AS $body$
DECLARE
data_cursor cursor for select * from test1;
I record;
BEGIN
    Open data_cursor;
    LOOP
       Fetch data_cursor INTO I;
      If not found then
            Exit;
      End if;
      Do something with I;
    END LOOP;
    Close data_cursor;
END;
$body$
LANGUAGE PLPGSQL;

In Oracle, cursors with the same name can be opened in recursively called functions. However, this is not allowed in AnalyticDB for PostgreSQL. Equivalent statements in AnalyticDB for PostgreSQL must be in the format of for i in query.

For example, convert the following:

FUNCTION test_func(level IN numer) IS
    Cursor data_cursor IS SELECT * from test1;
BEGIN
If level > 5 then
        return;
   End if;

    FOR I IN data_cursor LOOP
        Do something with I;
        test_func(level + 1);
END LOOP;
END;

To this code below:

CREATE OR REPLACE FUNCTION test_func(level int) returns void
AS $body$
DECLARE
data_cursor cursor for select * from test1;
I record;
BEGIN
    If level > 5 then
        return;
    End if;
    For I in select * from test1 LOOP
      Do something with I;
       PERFORM test_func(level+1);
    END LOOP;
END;
$body$
LANGUAGE PLPGSQL;

Community

Migrating Oracle PL/SQL Applications to AnalyticDB for PostgreSQL

The Open-source Ora2Pg Tool

Data Type Conversion Table

System Function Conversion Table

PL/SQL and PL/pgSQL

Package

Procedure/Function

PL Statement

For Statement

PRAGMA Statement

Transaction Processing

EXECUTE Statement

Pipe Row

Exception Handling

When Both Return and Out Parameters Are Included in a Function

When a Variable in a String Connection Contains an Apostrophe

Obtain the Days between Two Timestamps

PL Data Types

Record

Nested Table

Associative Array

Variable-Size Arrays

Global Variables

SQL

Connect By

Rownum

DUAL Table

User-Defined Functions in SELECT

(+) Multi-table Outer Join

Merge Into

Sequence

Cursor

Read previous post:

Michael Peng

You may also like

Comments

Michael Peng

Related Products

Oracle Database Migration Solution

Cloud Migration Solution

Hologres

ISV Solutions for Cloud Migration

User-Defined Functions in `SELECT`