The Alibaba Cloud 2021 Double 11 Cloud Services Sale is live now! For a limited time only you can turbocharge your cloud journey with core Alibaba Cloud products available from just $1, while you can win up to $1,111 in cash plus $1,111 in Alibaba Cloud credits in the Number Guessing Contest.
If you're a fan of police procedurals such as CSI, you've probably watched a scene where the police uses an image recognition software to identify a criminal based on a partial or blurry image. In the past, this process is done manually and is not very reliable. Now, we can use technologies such as PostgreSQL, which searches images in the database and finds a match based on similarity.
However, I don't want to talk about image searching today. Instead, I want to introduce text searching. Text searching may remind you about word segmentation, but word segmentation itself cannot meet all requirements. Why not? Well, let's look at a simple example where word segmentation fails: If a user types in "hello w0rld" instead of "hello world", how can the database match the text?
What about using a regular expression to match text? How can this be implemented? For example, if you type in a part of the domain name such as "firefox", how would the database determine that "www.firefoxcn.org" is the correct match?
When the data volume is small and concurrency is low, a full table scan can be performed for such a query and the CPU can afford the filtering for these queries. However, if the business needs to handle a hundred million requests or data every day, full table scan and the high CPU payload are unaffordable.
The details are provided in the pg_trgm code annotation, including four steps:
Create a test table including a character string type field. Insert 50 million random character strings.
postgres=# create extension pg_trgm;
postgres=# create table tbl(id int primary key, info text, crt_time timestamp);
postgres=# insert into tbl select id,md5(random()::text), now() from generate_series(1,50000000) t(id); Create the index supporting regular expression.
postgres=# CREATE INDEX trgm_idx_tbl_gin ON tbl USING GIN (info gin_trgm_ops); I have just shown the regular expression query to my colleague who works for other types of databases, and he was shocked by the speedy query.
postgres=# select * from tbl where info ~ '53?6b.*8823a' limit 10;
id | info | crt_time
----------+----------------------------------+----------------------------
4587797 | 0b1e56bd258823a9f9338919617651e5 | 2016-11-18 14:43:25.726919
7269097 | 9d5a7aace4bb56b29fe54cd98823a8ec | 2016-11-18 14:43:25.726919
11589980 | 3536b69b29b607348823a675cf4842c3 | 2016-11-18 14:43:25.726919
(3 rows)
Time: 142.087 ms
postgres=# explain (analyze,verbose,timing,costs,buffers) select * from tbl where info ~ '53?6b.*8823a' limit 10;
QUERY PLAN
------------------------------------------------------------------------------------------------------------------------------------
Limit (cost=527.75..537.82 rows=10 width=45) (actual time=140.867..140.902 rows=3 loops=1)
Output: id, info, crt_time
Buffers: shared hit=911
-> Bitmap Heap Scan on public.tbl (cost=527.75..5564.25 rows=5000 width=45) (actual time=140.847..140.881 rows=3 loops=1)
Output: id, info, crt_time
Recheck Cond: (tbl.info ~ '53?6b.*8823a'::text)
Rows Removed by Index Recheck: 5
Heap Blocks: exact=8
Buffers: shared hit=911
-> Bitmap Index Scan on trgm_idx_tbl (cost=0.00..526.50 rows=5000 width=0) (actual time=140.832..140.832 rows=8 loops=1)
Index Cond: (tbl.info ~ '53?6b.*8823a'::text)
Buffers: shared hit=903
Planning time: 0.389 ms
Execution time: 140.928 ms
(14 rows)
postgres=# select * from tbl where info ~ 'hello.*[a-f]{1}abc' limit 10;
id | info | crt_time
----+------+----------
(0 rows)
Time: 0.974 ms
postgres=# explain (analyze,verbose,timing,costs,buffers) select * from tbl where info ~ 'hello.*[a-f]{1}abc' limit 10;
QUERY PLAN
--------------------------------------------------------------------------------------------------------------------------------
Limit (cost=852.75..862.82 rows=10 width=45) (actual time=0.451..0.451 rows=0 loops=1)
Output: id, info, crt_time
Buffers: shared hit=35
-> Bitmap Heap Scan on public.tbl (cost=852.75..5889.25 rows=5000 width=45) (actual time=0.449..0.449 rows=0 loops=1)
Output: id, info, crt_time
Recheck Cond: (tbl.info ~ 'hello.*[a-f]{1}abc'::text)
Buffers: shared hit=35
-> Bitmap Index Scan on trgm_idx_tbl (cost=0.00..851.50 rows=5000 width=0) (actual time=0.447..0.447 rows=0 loops=1)
Index Cond: (tbl.info ~ 'hello.*[a-f]{1}abc'::text)
Buffers: shared hit=35
Planning time: 0.366 ms
Execution time: 0.479 ms
(12 rows)Fuzzy query example (Actually, regular expression query includes fuzzy match. Here is a demonstration.)
postgres=# select * from tbl where info ~ '821b8b92' limit 10;
id | info | crt_time
----+----------------------------------+----------------------------
4 | c5132821b8b92ba36487d06b438d8aed | 2016-11-18 14:43:25.726919
(1 row)
Time: 141.353 ms
postgres=# explain (analyze,verbose,timing,costs,buffers) select * from tbl where info ~ '821b8b92' limit 10;
QUERY PLAN
------------------------------------------------------------------------------------------------------------------------------------
Limit (cost=527.75..537.82 rows=10 width=45) (actual time=140.293..140.299 rows=1 loops=1)
Output: id, info, crt_time
Buffers: shared hit=904
-> Bitmap Heap Scan on public.tbl (cost=527.75..5564.25 rows=5000 width=45) (actual time=140.291..140.297 rows=1 loops=1)
Output: id, info, crt_time
Recheck Cond: (tbl.info ~ '821b8b92'::text)
Rows Removed by Index Recheck: 1
Heap Blocks: exact=2
Buffers: shared hit=904
-> Bitmap Index Scan on trgm_idx_tbl (cost=0.00..526.50 rows=5000 width=0) (actual time=140.279..140.279 rows=2 loops=1)
Index Cond: (tbl.info ~ '821b8b92'::text)
Buffers: shared hit=902
Planning time: 0.331 ms
Execution time: 140.323 ms
(14 rows)The consumed time in the preceding example is calculated in the full table scan scenario. The CPU parallel computing supported by PG is not used in this example.
postgres=# select * from tbl where info ~ '53?6b.*8823a' limit 10;
id | info | crt_time
----------+----------------------------------+----------------------------
4587797 | 0b1e56bd258823a9f9338919617651e5 | 2016-11-18 14:43:25.726919
7269097 | 9d5a7aace4bb56b29fe54cd98823a8ec | 2016-11-18 14:43:25.726919
11589980 | 3536b69b29b607348823a675cf4842c3 | 2016-11-18 14:43:25.726919
(3 rows)
Time: 93489.353 ms
postgres=# select * from tbl where info ~ 'hello.*[a-f]{1}abc' limit 10;
id | info | crt_time
----+------+----------
(0 rows)
Time: 78246.122 ms
postgres=# select * from tbl where info ~ '821b8b92' limit 10;
id | info | crt_time
----+----------------------------------+----------------------------
4 | c5132821b8b92ba36487d06b438d8aed | 2016-11-18 14:43:25.726919
(1 row)
Time: 82218.218 ms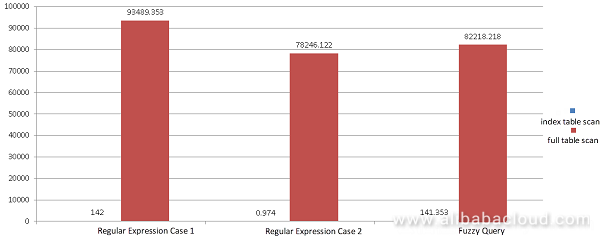
Here, GIN indexing is performed on tokens. When the character string is longer, more tokens are used. If the index field is updated, GIN asynchronous merging needs to be optimized to improve the update performance.
https://www.postgresql.org/docs/9.6/static/sql-createindex.html
GIN indexes accept different parameters:
fastupdate
This setting controls usage of the fast update technique described in Section 63.4.1.
It is a Boolean parameter: ON enables fast update, OFF disables it.
(Alternative spellings of ON and OFF are allowed as described in Section 19.1.) The default is ON.
gin_pending_list_limit
Custom gin_pending_list_limit parameter. This value is specified in kilobytes.Similarity-based query means that the database can match the input even if the text is incorrectly typed in. You may not remember every detail when doing a character puzzle or writing memoirs. In this situation, similarity-based query is useful.
/*-------------------------------------------------------------------------
*
* trgm_regexp.c
* Regular expression matching using trigrams.
*
* The general idea of trigram index support for a regular expression (regex)
* search is to transform the regex into a logical expression on trigrams.
* For example:
*
* (ab|cd)efg => ((abe & bef) | (cde & def)) & efg
*
* If a string matches the regex, then it must match the logical expression on
* trigrams. The opposite is not necessarily true, however: a string that
* matches the logical expression might not match the original regex. Such
* false positives are removed via recheck, by running the regular regex match
* operator on the retrieved heap tuple.
*
* Since the trigram expression involves both AND and OR operators, we can't
* expect the core index machinery to evaluate it completely. Instead, the
* result of regex analysis is a list of trigrams to be sought in the index,
* plus a simplified graph that is used by trigramsMatchGraph() to determine
* whether a particular indexed value matches the expression.
*
* Converting a regex to a trigram expression is based on analysis of an
* automaton corresponding to the regex. The algorithm consists of four
* stages:
*
* 1) Compile the regexp to NFA form. This is handled by the PostgreSQL
* regexp library, which provides accessors for its opaque regex_t struct
* to expose the NFA state graph and the "colors" (sets of equivalent
* characters) used as state transition labels.
*
* 2) Transform the original NFA into an expanded graph, where arcs
* are labeled with trigrams that must be present in order to move from
* one state to another via the arcs. The trigrams used in this stage
* consist of colors, not characters, as in the original NFA.
*
* 3) Expand the color trigrams into regular trigrams consisting of
* characters. If too many distinct trigrams are produced, trigrams are
* eliminated and the graph is simplified until it's simple enough.
*
* 4) Finally, the resulting graph is packed into a TrgmPackedGraph struct,
* and returned to the caller.
*
* 1) Compile the regexp to NFA form
* ---------------------------------
* The automaton returned by the regexp compiler is a graph where vertices
* are "states" and arcs are labeled with colors. Each color represents
* a set of characters, so that all characters assigned to the same color
* are interchangeable, so far as matching the regexp is concerned. There
* are two special states: "initial" and "final". A state can have multiple
* outgoing arcs labeled with the same color, which makes the automaton
* non-deterministic, because it can be in many states simultaneously.
*
* Note that this NFA is already lossy compared to the original regexp,
* since it ignores some regex features such as lookahead constraints and
* backref matching. This is OK for our purposes since it's still the case
* that only strings matching the NFA can possibly satisfy the regexp.
*
* 2) Transform the original NFA into an expanded graph
* ----------------------------------------------------
* In the 2nd stage, the automaton is transformed into a graph based on the
* original NFA. Each state in the expanded graph represents a state from
* the original NFA, plus a prefix identifying the last two characters
* (colors, to be precise) seen before entering the state. There can be
* multiple states in the expanded graph for each state in the original NFA,
* depending on what characters can precede it. A prefix position can be
* "unknown" if it's uncertain what the preceding character was, or "blank"
* if the character was a non-word character (we don't need to distinguish
* which non-word character it was, so just think of all of them as blanks).
*
* For convenience in description, call an expanded-state identifier
* (two prefix colors plus a state number from the original NFA) an
* "enter key".
*
* Each arc of the expanded graph is labelled with a trigram that must be
* present in the string to match. We can construct this from an out-arc of
* the underlying NFA state by combining the expanded state's prefix with the
* color label of the underlying out-arc, if neither prefix position is
* "unknown". But note that some of the colors in the trigram might be
* "blank". This is OK since we want to generate word-boundary trigrams as
* the regular trigram machinery would, if we know that some word characters
* must be adjacent to a word boundary in all strings matching the NFA.
*
* The expanded graph can also have fewer states than the original NFA,
* because we don't bother to make a separate state entry unless the state
* is reachable by a valid arc. When an enter key is reachable from a state
* of the expanded graph, but we do not know a complete trigram associated
* with that transition, we cannot make a valid arc; instead we insert the
* enter key into the enterKeys list of the source state. This effectively
* means that the two expanded states are not reliably distinguishable based
* on examining trigrams.
*
* So the expanded graph resembles the original NFA, but the arcs are
* labeled with trigrams instead of individual characters, and there may be
* more or fewer states. It is a lossy representation of the original NFA:
* any string that matches the original regexp must match the expanded graph,
* but the reverse is not true.
*
* We build the expanded graph through a breadth-first traversal of states
* reachable from the initial state. At each reachable state, we identify the
* states reachable from it without traversing a predictable trigram, and add
* those states' enter keys to the current state. Then we generate all
* out-arcs leading out of this collection of states that have predictable
* trigrams, adding their target states to the queue of states to examine.
*
* When building the graph, if the number of states or arcs exceed pre-defined
* limits, we give up and simply mark any states not yet processed as final
* states. Roughly speaking, that means that we make use of some portion from
* the beginning of the regexp. Also, any colors that have too many member
* characters are treated as "unknown", so that we can't derive trigrams
* from them.
*
* 3) Expand the color trigrams into regular trigrams
* --------------------------------------------------
* The trigrams in the expanded graph are "color trigrams", consisting
* of three consecutive colors that must be present in the string. But for
* search, we need regular trigrams consisting of characters. In the 3rd
* stage, the color trigrams are expanded into regular trigrams. Since each
* color can represent many characters, the total number of regular trigrams
* after expansion could be very large. Because searching the index for
* thousands of trigrams would be slow, and would likely produce so many
* false positives that we would have to traverse a large fraction of the
* index, the graph is simplified further in a lossy fashion by removing
* color trigrams. When a color trigram is removed, the states connected by
* any arcs labelled with that trigram are merged.
*
* Trigrams do not all have equivalent value for searching: some of them are
* more frequent and some of them are less frequent. Ideally, we would like
* to know the distribution of trigrams, but we don't. But because of padding
* we know for sure that the empty character is more frequent than others,
* so we can penalize trigrams according to presence of whitespace. The
* penalty assigned to each color trigram is the number of simple trigrams
* it would produce, times the penalties[] multiplier associated with its
* whitespace content. (The penalties[] constants were calculated by analysis
* of some real-life text.) We eliminate color trigrams starting with the
* highest-penalty one, until we get to a total penalty of no more than
* WISH_TRGM_PENALTY. However, we cannot remove a color trigram if that would
* lead to merging the initial and final states, so we may not be able to
* reach WISH_TRGM_PENALTY. It's still okay so long as we have no more than
* MAX_TRGM_COUNT simple trigrams in total, otherwise we fail.
*
* 4) Pack the graph into a compact representation
* -----------------------------------------------
* The 2nd and 3rd stages might have eliminated or merged many of the states
* and trigrams created earlier, so in this final stage, the graph is
* compacted and packed into a simpler struct that contains only the
* information needed to evaluate it.
*
* ALGORITHM EXAMPLE:
*
* Consider the example regex "ab[cd]". This regex is transformed into the
* following NFA (for simplicity we show colors as their single members):
*
* 4#
* c/
* a b /
* 1* --- 2 ---- 3
* \
* d\
* 5#
*
* We use * to mark initial state and # to mark final state. It's not depicted,
* but states 1, 4, 5 have self-referencing arcs for all possible characters,
* because this pattern can match to any part of a string.
*
* As the result of stage 2 we will have the following graph:
*
* abc abd
* 2# <---- 1* ----> 3#
*
* The process for generating this graph is:
* 1) Create state 1 with enter key (UNKNOWN, UNKNOWN, 1).
* 2) Add key (UNKNOWN, "a", 2) to state 1.
* 3) Add key ("a", "b", 3) to state 1.
* 4) Create new state 2 with enter key ("b", "c", 4). Add an arc
* from state 1 to state 2 with label trigram "abc".
* 5) Mark state 2 final because state 4 of source NFA is marked as final.
* 6) Create new state 3 with enter key ("b", "d", 5). Add an arc
* from state 1 to state 3 with label trigram "abd".
* 7) Mark state 3 final because state 5 of source NFA is marked as final.
*
*-------------------------------------------------------------------------
*/Double Eleven Technology Series: Logistics and Dynamic Path Planning
Supporting 200 Billion Data Records in a Single RDS PostgreSQL Instance
digoal - October 22, 2018
digoal - December 11, 2019
Alibaba F(x) Team - February 25, 2021
ApsaraDB - June 15, 2023
Alibaba Clouder - July 16, 2018
digoal - February 5, 2020
 Black Friday Cloud Services Sale
Black Friday Cloud Services Sale
Get started on cloud with $1. Start your cloud innovation journey here and now.
Learn More PolarDB for PostgreSQL
PolarDB for PostgreSQL
Alibaba Cloud PolarDB for PostgreSQL is an in-house relational database service 100% compatible with PostgreSQL and highly compatible with the Oracle syntax.
Learn More Database Overview
Database Overview
ApsaraDB: Faster, Stronger, More Secure
Learn MoreMore Posts by digoal