By digoal
The previous two articles introduced one-dimensional linear regression for stock price prediction, so only one independent variable was used. It is inaccurate to predict today's closing price based on yesterday’s closing price using a single element unless the results primarily depend on independent variables.
Multiple regression predicts more accurate results when the results depend on more than one variable. For example, you can use ternary regression to predict the next day's closing price based on yesterday's volume, closing price, and opening price.
In PostgreSQL, you can implement multiple linear regression using the MADlib library.
Example:
The Formula of P-variables Linear Regression:
y1=b0+b1x11+b2x12+…+bpx1p+ε1
y2=b0+b1x21+b2x22+…+bpx2p+ε2
……………… 1) Obtain intercept and slope.
2) Predict yn.
yn=b0+b1xn1+b2xn2+…+bpxnp+εn R Formula:
lm(y: 收盘价 ~ x1: 昨日收盘价 + x2: 昨日成交量, $DATA) 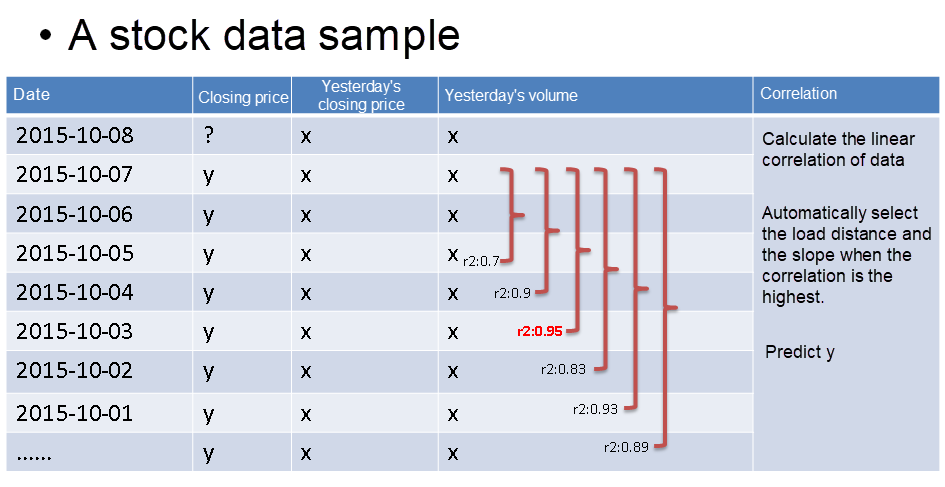
Practical example: http://doc.madlib.net/latest/group__grp__linreg.html
Create an input data set.
CREATE TABLE houses (id INT, tax INT, bedroom INT, bath FLOAT, price INT,
size INT, lot INT);
COPY houses FROM STDIN WITH DELIMITER '|';
1 | 590 | 2 | 1 | 50000 | 770 | 22100
2 | 1050 | 3 | 2 | 85000 | 1410 | 12000
3 | 20 | 3 | 1 | 22500 | 1060 | 3500
4 | 870 | 2 | 2 | 90000 | 1300 | 17500
5 | 1320 | 3 | 2 | 133000 | 1500 | 30000
6 | 1350 | 2 | 1 | 90500 | 820 | 25700
7 | 2790 | 3 | 2.5 | 260000 | 2130 | 25000
8 | 680 | 2 | 1 | 142500 | 1170 | 22000
9 | 1840 | 3 | 2 | 160000 | 1500 | 19000
10 | 3680 | 4 | 2 | 240000 | 2790 | 20000
11 | 1660 | 3 | 1 | 87000 | 1030 | 17500
12 | 1620 | 3 | 2 | 118600 | 1250 | 20000
13 | 3100 | 3 | 2 | 140000 | 1760 | 38000
14 | 2070 | 2 | 3 | 148000 | 1550 | 14000
15 | 650 | 3 | 1.5 | 65000 | 1450 | 12000
\. Prediction model:
linregr_train( source_table,
out_table,
dependent_varname,
independent_varname,
grouping_cols, -- 可选
heteroskedasticity_option -- 可选
)
Train a regression model. First, a single regression for all the data. The “houses” contain historical data, including independent variables and dependent variables. Price is a dependent variable, and tax, bath, and size are independent variables. This is so-called ternary linear regression.
The “houses_linregr” stores the linear regression statistics, including correlation, R2, standard deviation, P value, etc.
SELECT madlib.linregr_train( 'houses',
'houses_linregr',
'price',
'ARRAY[1, tax, bath, size]'
); It is feasible to add grouping fields when group predictions based on source data are required.
Generate three output models, one for each value of "bedroom".
SELECT madlib.linregr_train( 'houses',
'houses_linregr_bedroom',
'price',
'ARRAY[1, tax, bath, size]',
'bedroom'
);
Examine the resulting models.
-- Set extended display on for easier reading of output
\x ON
SELECT * FROM houses_linregr;
Result:
-[ RECORD 1 ]+---------------------------------------------------------------------------
coef | {-12849.4168959872,28.9613922651765,10181.6290712648,50.516894915354}
r2 | 0.768577580597443
std_err | {33453.0344331391,15.8992104963997,19437.7710925923,32.928023174087}
t_stats | {-0.38410317968819,1.82156166004184,0.523806408809133,1.53416118083605}
p_values | {0.708223134615422,0.0958005827189772,0.610804093526536,0.153235085548186}
condition_no | 9002.50457085737 The value of R2 is 0.76, meaning its correlation is poor. So, dynamic data segment computing mentioned earlier is needed for good correlation.
View the results grouped by bedroom.
SELECT * FROM houses_linregr_bedroom;
Result:
-[ RECORD 1 ]+--------------------------------------------------------------------------
bedroom | 2
coef | {-84242.0345406597,55.4430144648696,-78966.9753675319,225.611910021192}
r2 | 0.968809546465313
std_err | {35018.9991665742,19.5731125320686,23036.8071292552,49.0448678148784}
t_stats | {-2.40560942761235,2.83261103077151,-3.42786111480046,4.60011251070697}
p_values | {0.250804617665239,0.21605133377602,0.180704400437373,0.136272031474122}
condition_no | 10086.1048721726
-[ RECORD 2 ]+--------------------------------------------------------------------------
bedroom | 4
coef | {0.0112536020318378,41.4132554771633,0.0225072040636757,31.3975496688276}
r2 | 1
std_err | {0,0,0,0}
t_stats | {Infinity,Infinity,Infinity,Infinity}
p_values |
condition_no | Infinity
-[ RECORD 3 ]+--------------------------------------------------------------------------
bedroom | 3
coef | {-88155.8292501601,27.1966436294429,41404.0293363612,62.637521075324}
r2 | 0.841699901311252
std_err | {57867.9999702625,17.8272309154689,43643.1321511114,70.8506824863954}
t_stats | {-1.52339512849005,1.52556747362508,0.948695185143966,0.884077878676067}
p_values | {0.188161432894871,0.187636685729869,0.386340032374927,0.417132778705789}
condition_no | 11722.6225642147
Alternatively you can unnest the results for easier reading of output.
\x OFF
SELECT unnest(ARRAY['intercept','tax','bath','size']) as attribute,
unnest(coef) as coefficient,
unnest(std_err) as standard_error,
unnest(t_stats) as t_stat,
unnest(p_values) as pvalue
FROM houses_linregr;
Use the prediction function to evaluate residuals.
SELECT houses.*,
madlib.linregr_predict( ARRAY[1,tax,bath,size],
m.coef
) as predict,
price -
madlib.linregr_predict( ARRAY[1,tax,bath,size],
m.coef
) as residual
FROM houses, houses_linregr m; After obtaining a good correlation of R2, this set of data can predict the next data set.
PostgreSQL: High Availability and Disaster Recovery Solutions for the Financial Industry
PostgreSQL: How to Predict Stock Price Using Univariate Linear Regression
digoal - April 27, 2021
digoal - May 16, 2019
digoal - April 23, 2021
digoal - May 16, 2019
digoal - April 23, 2021
Alibaba Clouder - August 12, 2020
 PolarDB for PostgreSQL
PolarDB for PostgreSQL
Alibaba Cloud PolarDB for PostgreSQL is an in-house relational database service 100% compatible with PostgreSQL and highly compatible with the Oracle syntax.
Learn More Quick BI
Quick BI
A new generation of business Intelligence services on the cloud
Learn More AnalyticDB for PostgreSQL
AnalyticDB for PostgreSQL
An online MPP warehousing service based on the Greenplum Database open source program
Learn More Time Series Database (TSDB)
Time Series Database (TSDB)
TSDB is a stable, reliable, and cost-effective online high-performance time series database service.
Learn MoreMore Posts by digoal