PostgreSQL: Performing Linear Regression Analysis to Predict Future Data (Part 1)

By digoal

Background

To start with, let's read a story about linear regression analysis and the least-squares method. (Excerpted from Baidu)

In 1801, Italian astronomer Giuseppe Piazzi found the first asteroid called Ceres. After 40 days of tracking and observation, Giuseppe Piazzi lost its location because Ceres ran to the sun’s rear. Later, scientists worldwide tried to find Ceres based on the observation data provided by Giuseppe Piazzi. However, Ceres was not found based on the computing results of most scientists. Gauss, who was 24 years old at that time, also calculated the orbit of Ceres. Based on the orbit data that Gauss calculated, Austrian astronomer Heinrich Olbers found Ceres.

The least-squares method Gauss used for tracking Ceres was published in his book Theory of the Motion of the Heavenly Bodies Moving about the Sun in Conic Sections in 1809.

The French scientist Legendre independently discovered the least-squares method in 1806, but he remained unknown as people had no idea about his discovery at that time.

Legendre once had a dispute with Gauss about who was the first discoverer of the least-squares method.

In 1829, Gauss proved that the least-squares method’s optimization is better than other methods, so it is called the Gauss-Markov theorem.

This story shows that we can predict future data from existing data. However, there are uncertain factors determining whether the prediction results are accurate or not, so continuous adjustment and verification are needed.

How can we perform a regression analysis? (Excerpted from Baidu)

For one or more random variables denoted by Yi and other variables denoted by Xk, the statistical method used to study their relationship is called multiple regression analysis. Yi is the dependent variable, and Xk is the independent variable. The regression analysis is a kind of mathematical model. The special linear model indicates that the relationship between the dependent variable and the independent variable is linear.

The simplest regression analysis is called simple linear regression, in which an independent variable and a dependent variable have a linear relationship in general. The model is Y = a + bX + ε, where X is the independent variable, Y is the dependent variable, and ε is the random error.

Generally, it is assumed that the mean value of the random error is 0, and the variance is σ^2 (σ^2 is greater than 0), and σ^2 has nothing to do with the value of X. If the random error is further assumed to follow the normal distribution, it is called a normal linear model. In general, it has k number of independent variables and one dependent variable.

We can divide the dependent variable’s value into two parts: One is expressed as a function of the independent variable due to its influence. The form of the function is known, but it contains some unknown parameters. The other is the random error due to the influence of other unconsidered factors and randomness. The linear function with unknown parameters is called the linear regression analysis model, and the nonlinear function with unknown parameters is called the nonlinear regression analysis model. The model is called multivariable regression when the number of independent variables is greater than 1 and multiple regression when the number of dependent variables is greater than 1.

The primary process of the regression analysis is as follows:

1) To determine the quantitative relation between certain variables from a set of data, that is, to establish a mathematical model and estimate the unknown parameters. The commonly used method for estimating parameters is the least-squares method.

2) To test the reliability of these relations.

3) To judge the influence of independent variables in the relationship that many independent variables jointly affect a dependent variable so that we can put those significant independent variables into the model while eliminating those non-significant independent variables. Generally, methods such as stepwise regression, forward regression, and backward regression are used.

4) To predict or control a certain production process using the obtained relation. Regression analysis is widely used, and statistical software packages make it very convenient to calculate data through various regression methods.

In regression analysis, variables are divided into two categories: One is the dependent variable, usually denoted by Y, which is typically a kind of indicator concerned with practical problems. The other is the independent variable denoted by X, which affects the value of the dependent variable.

The main aims of regression analysis are as follows:

1) To determine the quantitative relation expression between Y and X, which is a regression equation.

2) To test the reliability of the obtained regression equation.

3) To judge whether independent variable X influences dependent variable Y.

4) To predict and control future data by using the obtained regression equation.

Let's look at one example:

In practice, product quality will affect customer satisfaction. Therefore, when studying the causal relationship between product quality and customer satisfaction, we should set customer satisfaction as the dependent variable denoted by Y, and product quality as the independent variable denoted by X.

According to the scatter plot of Figure 8-3, we can establish the following linear relationship:

Y = A + BX + §

In the formula, A and B are undetermined parameters. A is the intercept of the regression line, and B is the slope of the regression line, indicating the average change of Y when X changes by one unit. § is a random error that depends on customer satisfaction.

An empirical regression equation is y = 0.857 + 0.836x.

The intercept of the regression line on the y-axis is 0.857 and the slope is 0.836, indicating customer satisfaction will increase by 0.836 points on average for each point of the quality improvement. In other words, the contribution of every 1 point increase in quality to customer satisfaction is 0.836 points.

PostgreSQL Functions Related to Linear Regression Analysis

PostgreSQL provides some aggregate functions for regression analysis.

Function	Parameter Type	Return Type	Description
regr_avgx(Y, X)	DOUBLE PRECISION	DOUBLE PRECISION	The average of the independent variable (sum(X)/N).
regr_avgy(Y, X)	DOUBLE PRECISION	DOUBLE PRECISION	The average of the dependent variable (sum(Y)/N).
regr_count(Y, X)	DOUBLE PRECISION	BIGINT	The number of input rows in which both expressions are nonnull.
regr_intercept(Y, X)	DOUBLE PRECISION	DOUBLE PRECISION	The y-intercept of the least-squares-fit linear equation determined by the (X, Y) pairs.
regr_r2(Y, X)	DOUBLE PRECISION	DOUBLE PRECISION	The square of the correlation coefficient.
regr_slope(Y, X)	DOUBLE PRECISION	DOUBLE PRECISION	The slope of the least-squares-fit linear equation determined by the (X, Y) pairs.
regr_sxx(Y, X)	DOUBLE PRECISION	DOUBLE PRECISION	Sum (X^2 ) - sum (X)^2/N("sum of squares" of the independent variable)
regr_sxy(Y, X)	DOUBLE PRECISION	DOUBLE PRECISION	Sum (XY) - sum (X) sum(Y)/N ("sum of products" of independent times dependent variable)
regr_syy(Y, X)	DOUBLE PRECISION	DOUBLE PRECISION	Sum (Y2) - sum(Y)^2/N ("sum of squares" of the dependent variable)

The following functions are used in this article:

regr_intercept is used to calculate the intercept.
regr_slope is used to calculate the slope.
regr_r2 is used to calculate the correlation. The higher the correlation is, the more accurate the prediction.

Let's look at an actual case.

First, put the last year’s daily visit data of a business into a test table.

Second, perform a simple regression analysis on the data. The dependent variable is what we will predict, and the independent variable is what we will use for prediction. Because the data to be predicted does not exist, we can use the next day’s dependent variable as today’s independent variable.

In the following table, independent variables are generated when the data is moved down a row.

Dependent Variable	Independent Variable
48,000	54624
47454	48,000
56766	47454
60488	56766
58191	60488
57443	58191
54277	57443
55508	54277
52716	55508
63748	52716
43462	63748
44248	43462
40145	44248

If multiple influencing factors exist and multi-regression is required, we can use the R programming language plug-in in PostgreSQL or MADlib's training function for analysis.

This article demonstrates the simple regression analysis.

First, create a table that stores a business’s daily download volume in the past 365 days.

digoal=> create table test as select row_number() over(order by dt) as rn,cnt from   
         (select date(createtime) as dt, count(*) as cnt from tbl_app_download where createtime>=( date(now())-366 ) and createtime<( date(now())-1 ) group by date(createtime)) as t;  
SELECT 365

The data looks like this:

digoal=> select * from test;  
....  
 329 | 36293  
 330 | 40886  
 331 | 34465  
 332 | 30785  
 333 | 33318  
 334 | 34480  
....

Second, test the linear correlation of regression in different data ranges.

For example, to calculate the regression linear correlation for data in the last 362 days, and the result is as follows:

digoal=> select count(*),regr_r2(t.cnt,test.cnt) from   
(select rn-1 as rn,cnt from test) as t,test where t.rn=test.rn and test.rn>2;  
 count | regr_r2        
-------+ -------------------  
   362 | 0.835282212765017  
(1 row)

However, if the time span is enlarged to the last 363 days, the correlation gets reduced to 0.32915622582628.

digoal=> select count(*),regr_r2(t.cnt,test.cnt) from   
(select rn-1 as rn,cnt from test) as t,test where t.rn=test.rn and test.rn>1;  
 count | regr_r2        
-------+ ------------------  
   363 | 0.32915622582628  
(1 row)

Therefore, we need to attempt constantly to get a better correlation. The prediction is the most accurate when we obtain the highest correlation (close to 1).

Let's look at the prediction accuracy of the intercept and slope generated in the two time periods mentioned above.

Intercept:

digoal=> select count(*),regr_intercept(t.cnt,test.cnt) from   
(select rn-1 as rn,cnt from test) as t,test where t.rn=test.rn and test.rn>2;  
 count | regr_intercept    
-------+ ------------------  
   362 | 6274.25023499543  
(1 row)

Slope:

digoal=> select count(*),regr_slope(t.cnt,test.cnt) from       
(select rn-1 as rn,cnt from test) as t,test where t.rn=test.rn and test.rn>2;  
 count | regr_slope       
-------+ -------------------  
   362 | 0.906861594725424  
(1 row)

Use the independent variable of 44248 to speculate the dependent variable of 40145.

The result is 46401.062078405991152 by using the formula.

digoal=> select 44248*0.906861594725424+6274.25023499543;  
       ? column?          
-----------------------  
 46401.062078405991152  
(1 row)

Accuracy:

digoal=> select 40145/46401.062078405991152;  
        ? column?          
------------------------  
 0.86517416200873079820  
(1 row)

When we use another set of intercepts and slopes, the minimum accuracy is 0.32915622582628. Therefore, predicted results might not be as good as the examples mentioned above.

Intercept:

digoal=> select count(*),regr_intercept(t.cnt,test.cnt) from   
(select rn-1 as rn,cnt from test) as t,test where t.rn=test.rn and test.rn>1;  
 count | regr_intercept    
-------+ ------------------  
   363 | 49279.0342891155  
(1 row)

Slope:

digoal=> select count(*),regr_slope(t.cnt,test.cnt) from       
(select rn-1 as rn,cnt from test) as t,test where t.rn=test.rn and test.rn>1;  
 count | regr_slope       
-------+ -------------------  
   363 | 0.292250474909646  
(1 row)

Prediction results:

digoal=> select 44248*0.292250474909646+49279.0342891155;  
       ? column?          
-----------------------  
 62210.533302917516208  
(1 row)

Accuracy:

digoal=> select 40145/62210.533302917516208;  
        ? column?          
------------------------  
 0.64530872616900233730  
(1 row)

Next, let's discuss several other regression-related functions.

regr_avgx(y, x): This function aims to calculate the average value of x (mathematical expectation), and y has no effect here.
regr_avgy(y, x): This function aims to calculate the average value of y (mathematical expectation), and x has no effect here.
regr_count(y, x): This function aims to calculate the number of records in which neither x nor y is empty.

The other three are auxiliary functions that calculate diagnostic statistics (total variance, total covariance).

regr_sxx(y, x) : sum(X^2) - sum(X)^2/N   
regr_sxy(y, x) : sum(X*Y) - sum(X) * sum(Y)/N  
regr_syy(y, x) : sum(Y^2) - sum(Y)^2/N   
  
REGR_SXY, REGR_SXX, REGR_SYY are auxiliary functions that are used to compute various diagnostic statistics.  
REGR_SXX makes the following computation after the elimination of null (expr1, expr2) pairs:  
REGR_COUNT(expr1, expr2) * VAR_POP(expr2)  
  
REGR_SYY makes the following computation after the elimination of null (expr1, expr2) pairs:  
REGR_COUNT(expr1, expr2) * VAR_POP(expr1)  
  
REGR_SXY makes the following computation after the elimination of null (expr1, expr2) pairs:  
REGR_COUNT(expr1, expr2) * COVAR_POP(expr1, expr2)

To verify regr_sxx, sxy, syy:

postgres=# select regr_sxx(y,x), REGR_COUNT(y,x)*VAR_POP(x) from (values(2,400),(6,401),(7,400),(3,400),(1000,488)) as t(x,y);  
 regr_sxx |? column?         
----------+ ---------------------  
 792833.2 | 792833.200000000000  
(1 row)  
  
postgres=# select regr_sxy(y,x), REGR_COUNT(y,x)*COVAR_POP(x,y) from (values(2,400),(6,401),(7,400),(3,400),(1000,488)) as t(x,y);  
 regr_sxy |? column?   
--------+----------  
  69885.6 | 69885.6  
(1 row)  
  
postgres=# select regr_syy(y,x), REGR_COUNT(y,x)*VAR_POP(y) from (values(2,400),(6,401),(7,400),(3,400),(1000,488)) as t(x,y);  
 regr_syy |? column?          
+----------+-----+----------------------- -+  
   6160.8 | 6160.8000000000000000  
(1 row)

Well, that's all about the regression analysis. We encouraged further exploration about this.

Examples of automatic optimal selection are as follows:

=> select * from test order by to_char desc limit 10;  
  to_char | count    
------------+ --------  
 2015030123 | 149496  
 2015030122 | 165320  
 2015030121 | 167663  
 2015030120 | 161071  
 2015030119 | 145570  
 2015030118 | 133155  
 2015030117 | 133962  
 2015030116 | 130484  
 2015030115 | 126182  
 2015030114 | 122998  
(10 rows)  
  
do language plpgsql $$                           
declare   
  r2_1 numeric := 0;   
  r2_2 numeric := 0;   
  var int;  
  inter numeric;  
  slope numeric;  
  inter_2 numeric;  
  slope_2 numeric;  
  realv numeric;  
  predicv numeric;  
  offset_var int := 0; --最后一个值的预测值
begin  
  for i in 1..len loop  
    with t1 as (select row_number() over(order by to_char) as rn,count from test order by to_char desc offset offset_var)   
         t2 as (select row_number() over(order by to_char)-1 as rn,count from test order by to_char desc offset offset_var)    
      select regr_intercept(t2.count,t1.count),regr_slope(t2.count,t1.count),regr_r2(t1.count,t2.count) into inter,slope,r2_1 from t1,t2 where t1.rn=t2.rn and t1.rn> I;   
    if r2_1>r2_2 then   
      inter_2:=inter;  
      slope_2:=slope;  
      r2_2:=r2_1;   
      var:= I;  
    end if;   
  end loop;   
  
  raise notice '%, %, %, %', var, inter_2,slope_2,r2_2;  
  select slope_2*count+inter_2 into predicv from test order by to_char desc offset offset_var+1 limit 1;  
  select count into realv from test order by to_char desc offset offset_var limit 1;  
  raise notice '%, %', realv, predicv;  
end;  
$$;  
NOTICE: 436, 16599.0041292694, 0.896184690654355, 0.925125327496365  
NOTICE: 149496, 164756.257188247368600  
DO  
  
=> select 149496/164756.2;  
        ? column?          
------------------------  
 0.90737708201572990880  
(1 row)  
  
do language plpgsql $$                           
declare   
  r2_1 numeric := 0; --相关性   
  r2_2 numeric := 0; --最大相关性 
  var int; --样本数量
  inter_1 numeric; --截距
  Lopez_1 numeric; --斜率
  inter_2 numeric; --最大相关性截距    
  Sleepe_2 numeric; --最大相关性斜率    
  realv numeric; --真实数据  
  predicv numeric; --预测数据   
  offset_var int := 1; --倒数第二个值的预测值, 不停迭代, 最后计算所有的实际值和预测值的corr, 看看相似度如何?
begin  
  for i in 1..len loop  
    with t1 as (select row_number() over(order by to_char) as rn,count from test order by to_char desc offset offset_var)   
         t2 as (select row_number() over(order by to_char)-1 as rn,count from test order by to_char desc offset offset_var)   
      select regr_intercept(t2.count,t1.count),regr_slope(t2.count,t1.count),regr_r2(t1.count,t2.count) into inter_1,slope_1,r2_1 from t1,t2 where t1.rn=t2.rn and t1.rn> I;  
    if r2_1>r2_2 then   
      inter_2 := inter_1;  
      slope_2 := slope_1;  
      r2_2 := r2_1;  
      var := I;  
    end if;  
  end loop;  
  
  raise notice '样本数量%, 截距%, 斜率%, 相关性% ', var, round(inter_2,4), round (SAPE__2,4), round(r2_2,4);  
  select slope_2*count+inter_2 into predicv from test order by to_char desc offset offset_var+1 limit 1;  
  select count into realv from test order by to_char desc offset offset_var limit 1;  
  raise notice'真实数据%, 预测数据%, 本次预测偏差,%%%', realv, round (prediction), abs(1-round (prediction/realv,4))* 100;  
end;  
$$;  
NOTICE: 样本数量436, 截距10109.8500, 斜率0.9573, 相关性0.9476  
NOTICE: 真实数据165320, 预测数据170611, 本次预测偏差,%3.2000 
DO

Function checksum:

=> create or replace function check_predict(IN ov int, OUT rv numeric, OUT pv numeric, OUT dev numeric) returns record as $$  
declare   
  r2_1 numeric := 0; --相关性
  r2_2 numeric := 0; --最大相关性
  var int; --样本数量  
  inter_1 numeric; --截距
  Lopez_1 numeric; --斜率
  inter_2 numeric; --最大相关性截距   
  Sleepe_2 numeric; --最大相关性斜率   
  realv numeric; --真实数据  
  predicv numeric; --预测数据  
  offset_var int := ov; --倒数第二个值的预测值, 不停迭代, 最后计算所有的实际值和预测值的corr, 看看相似度如何?  
  idx int := 0;  
begin  
  select count(*)-offset_var-4 into lps from test; --循环不要超过总样本数, 同时至少给2个样本.  
  for i in 1..len loop   
    with t1 as (select row_number() over(order by to_char) as rn,to_char,count from test order by to_char desc offset offset_var)   
         t2 as (select row_number() over(order by to_char)-1 as rn,to_char,count from test order by to_char desc offset offset_var)   
      select regr_intercept(t2.count,t1.count),regr_slope(t2.count,t1.count),regr_r2(t1.count,t2.count) into inter_1,slope_1,r2_1 from t1,t2 where t1.rn=t2.rn and t1.rn> I;  
    if r2_1>r2_2 then   
      inter_2 := inter_1;  
      slope_2 := slope_1;  
      r2_2 := r2_1;  
      var := I;  
    end if;  
  end loop;  
  
  raise notice '样本数量%, 截距%, 斜率%, 相关性%', var, round(inter_2,4), round (SAPE__2,4), round(r2_2,4);  
  select slope_2*count+inter_2 into predicv from test order by to_char desc offset offset_var+1 limit 1;  
  select count into realv from test order by to_char desc offset offset_var limit 1;  
  raise notice '真实数据%, 预测数据%, 本次预测偏差%%%', realv, round(predicv), abs(1-round(predicv/realv,4))* 100;  
  
  rv := realv;  
  pv := round(predicv);  
  dev := abs(1-round(predicv/realv,4));  
  return;  
end;  
language plpgsql;

Checksum test:

=> select check_predict( I) from generate_series(1,100) t( I);  
NOTICE:  样本数量436, 截距10109.8500, 斜率0.9573, 相关性0.9476  
NOTICE:  真实数据165320, 预测数据170611, 本次预测偏差%3.2000  
NOTICE:  样本数量436, 截距6909.3635, 斜率0.9872, 相关性0.9419  
NOTICE:  真实数据167663, 预测数据165922, 本次预测偏差%1.0400  
NOTICE:  样本数量436, 截距8151.8730, 斜率0.9754, 相关性0.9249  
NOTICE:  真实数据161071, 预测数据150145, 本次预测偏差%6.7800  
NOTICE:  样本数量436, 截距14388.5296, 斜率0.9135, 相关性0.9275  
NOTICE:  真实数据145570, 预测数据136026, 本次预测偏差%6.5600  
NOTICE:  样本数量437, 截距30451.0167, 斜率0.7726, 相关性0.9570  
NOTICE:  真实数据133155, 预测数据133953, 本次预测偏差%0.6000  
NOTICE:  样本数量446, 截距343.4262, 斜率1.0262, 相关性0.9785  
NOTICE:  真实数据133962, 预测数据134241, 本次预测偏差%0.2100  
NOTICE:  样本数量437, 截距31491.5019, 斜率0.7616, 相关性0.9494  
NOTICE:  真实数据130484, 预测数据127596, 本次预测偏差%2.2100  
NOTICE:  样本数量438, 截距48512.9273, 斜率0.6126, 相关性0.9484  
NOTICE:  真实数据126182, 预测数据123864, 本次预测偏差%1.8400  
NOTICE:  样本数量438, 截距50299.8161, 斜率0.5940, 相关性0.9526  
NOTICE:  真实数据122998, 预测数据124578, 本次预测偏差%1.2800  
NOTICE:  样本数量442, 截距33561.3690, 斜率0.7444, 相关性0.9983  
NOTICE:  真实数据125052, 预测数据125119, 本次预测偏差%0.0500  
NOTICE:  样本数量438, 截距50126.2968, 斜率0.5954, 相关性0.9475  
NOTICE:  真实数据123000, 预测数据121572, 本次预测偏差%1.1600  
NOTICE:  样本数量438, 截距52640.6564, 斜率0.5687, 相关性0.9400  
NOTICE:  真实数据119991, 预测数据118710, 本次预测偏差%1.0700  
NOTICE:  样本数量438, 截距55198.2911, 斜率0.5404, 相关性0.9301  
NOTICE:  真实数据116182, 预测数据118363, 本次预测偏差%1.8800  
NOTICE:  样本数量438, 截距43721.8498, 斜率0.6665, 相关性0.9845  
NOTICE:  真实数据116887, 预测数据116082, 本次预测偏差%0.6900  
NOTICE:  样本数量1, 截距4661.3951, 斜率0.9464, 相关性0.8978  
NOTICE:  真实数据108562, 预测数据98517, 本次预测偏差%9.2500  
NOTICE:  样本数量1, 截距4675.5276, 斜率0.9460, 相关性0.8979  
NOTICE:  真实数据99168, 预测数据82725, 本次预测偏差%16.5800  
NOTICE:  样本数量432, 截距39520.3078, 斜率0.4823, 相关性0.9201  
NOTICE:  真实数据82505, 预测数据74942, 本次预测偏差%9.1700  
NOTICE:  样本数量432, 截距31502.3387, 斜率0.5457, 相关性0.9985  
NOTICE:  真实数据73450, 预测数据72804, 本次预测偏差%0.8800  
NOTICE:  样本数量432, 截距30417.7790, 斜率0.5542, 相关性0.9989  
NOTICE:  真实数据75681, 预测数据76143, 本次预测偏差%0.6100  
NOTICE:  样本数量432, 截距31775.6232, 斜率0.5440, 相关性0.9992  
NOTICE:  真实数据82509, 预测数据82187, 本次预测偏差%0.3900  
NOTICE:  样本数量1, 截距4622.2503, 斜率0.9465, 相关性0.8993  
NOTICE:  真实数据92670, 预测数据111447, 本次预测偏差%20.2600  
NOTICE:  样本数量1, 截距4531.6850, 斜率0.9481, 相关性0.9003  
NOTICE:  真实数据112865, 预测数据145539, 本次预测偏差%28.9500  
NOTICE:  样本数量412, 截距19211.5611, 斜率0.8778, 相关性0.9590  
NOTICE:  真实数据148731, 预测数据150848, 本次预测偏差%1.4200  
NOTICE:  样本数量412, 截距18806.5399, 斜率0.8820, 相关性0.9580  
NOTICE:  真实数据149961, 预测数据156169, 本次预测偏差%4.1400  
NOTICE:  样本数量412, 截距17050.6057, 斜率0.8991, 相关性0.9603  
NOTICE:  真实数据155748, 预测数据161289, 本次预测偏差%3.5600  
NOTICE:  样本数量412, 截距14830.5241, 斜率0.9202, 相关性0.9607  
NOTICE:  真实数据160430, 预测数据155939, 本次预测偏差%2.8000  
NOTICE:  样本数量412, 截距16540.9704, 斜率0.9034, 相关性0.9574  
NOTICE:  真实数据153344, 预测数据150240, 本次预测偏差%2.0200  
NOTICE:  样本数量412, 截距17692.1060, 斜率0.8917, 相关性0.9532  
NOTICE:  真实数据147997, 预测数据140772, 本次预测偏差%4.8800  
NOTICE:  样本数量414, 截距41717.5731, 斜率0.6980, 相关性0.9736  
NOTICE:  真实数据138023, 预测数据137013, 本次预测偏差%0.7300  
NOTICE:  样本数量414, 截距42191.4454, 斜率0.6933, 相关性0.9722  
NOTICE:  真实数据136535, 预测数据135075, 本次预测偏差%1.0700  
NOTICE:  样本数量414, 截距42836.5141, 斜率0.6866, 相关性0.9716  
NOTICE:  真实数据133978, 预测数据133909, 本次预测偏差%0.0500  
NOTICE:  样本数量414, 截距42868.4919, 斜率0.6863, 相关性0.9698  
NOTICE:  真实数据132634, 预测数据136891, 本次预测偏差%3.2100  
NOTICE:  样本数量414, 截距39356.6117, 斜率0.7213, 相关性0.9849  
NOTICE:  真实数据136998, 预测数据137674, 本次预测偏差%0.4900  
NOTICE:  样本数量418, 截距-98886.5041, 斜率1.7965, 相关性0.9925  
NOTICE:  真实数据136303, 预测数据136431, 本次预测偏差%0.0900  
NOTICE:  样本数量414, 截距41274.0892, 斜率0.7011, 相关性0.9848  
NOTICE:  真实数据130987, 预测数据130817, 本次预测偏差%0.1300  
NOTICE:  样本数量414, 截距41537.1100, 斜率0.6983, 相关性0.9803  
NOTICE:  真实数据127722, 预测数据129731, 本次预测偏差%1.5700  
NOTICE:  样本数量414, 截距35567.9284, 斜率0.7625, 相关性0.9901  
NOTICE:  真实数据126303, 预测数据124949, 本次预测偏差%1.0700  
NOTICE:  样本数量414, 截距41599.7365, 斜率0.6944, 相关性0.9993  
NOTICE:  真实数据117218, 预测数据117405, 本次预测偏差%0.1600  
NOTICE:  样本数量413, 截距1686.3033, 斜率1.1262, 相关性0.8957  
NOTICE:  真实数据109160, 预测数据110726, 本次预测偏差%1.4300  
NOTICE:  样本数量412, 截距-126088.7154, 斜率2.7998, 相关性0.9671  
NOTICE:  真实数据96823, 预测数据97097, 本次预测偏差%0.2800  
NOTICE:  样本数量408, 截距36426.6219, 斜率0.5003, 相关性0.9205  
NOTICE:  真实数据79716, 预测数据72776, 本次预测偏差%8.7100  
NOTICE:  样本数量408, 截距29915.3284, 斜率0.5522, 相关性0.9813  
NOTICE:  真实数据72658, 预测数据69530, 本次预测偏差%4.3100  
NOTICE:  样本数量409, 截距30542.2158, 斜率0.5286, 相关性0.9970  
NOTICE:  真实数据71739, 预测数据71377, 本次预测偏差%0.5100  
NOTICE:  样本数量408, 截距21294.1724, 斜率0.6206, 相关性0.9985  
NOTICE:  真实数据77243, 预测数据76786, 本次预测偏差%0.5900  
NOTICE:  样本数量1, 截距4921.7169, 斜率0.9414, 相关性0.8898  
NOTICE:  真实数据89412, 预测数据109386, 本次预测偏差%22.3400  
NOTICE:  样本数量406, 截距-771730.9711, 斜率6.1383, 相关性0.9650  
NOTICE:  真实数据110972, 预测数据112269, 本次预测偏差%1.1700  
NOTICE:  样本数量388, 截距15580.3852, 斜率0.9001, 相关性0.9520  
NOTICE:  真实数据144014, 预测数据149237, 本次预测偏差%3.6300  
NOTICE:  样本数量388, 截距14377.9729, 斜率0.9129, 相关性0.9524  
NOTICE:  真实数据148483, 预测数据151688, 本次预测偏差%2.1600  
NOTICE:  样本数量388, 截距13455.2553, 斜率0.9226, 相关性0.9497  
NOTICE:  真实数据150405, 预测数据156324, 本次预测偏差%3.9400  
NOTICE:  样本数量402, 截距71505.3386, 斜率0.5561, 相关性0.9759  
NOTICE:  真实数据154850, 预测数据155607, 本次预测偏差%0.4900  
NOTICE:  样本数量388, 截距11270.4334, 斜率0.9451, 相关性0.9387  
NOTICE:  真实数据151244, 预测数据144638, 本次预测偏差%4.3700  
NOTICE:  样本数量388, 截距14060.3682, 斜率0.9147, 相关性0.9332  
NOTICE:  真实数据141118, 预测数据129415, 本次预测偏差%8.2900  
NOTICE:  样本数量390, 截距36957.1231, 斜率0.7099, 相关性0.9656  
NOTICE:  真实数据126106, 预测数据125617, 本次预测偏差%0.3900  
NOTICE:  样本数量390, 截距37150.1505, 斜率0.7077, 相关性0.9636  
NOTICE:  真实数据124896, 预测数据128489, 本次预测偏差%2.8800  
NOTICE:  样本数量390, 截距34760.7660, 斜率0.7330, 相关性0.9714  
NOTICE:  真实数据129061, 预测数据128477, 本次预测偏差%0.4500  
NOTICE:  样本数量390, 截距35229.1317, 斜率0.7280, 相关性0.9667  
NOTICE:  真实数据127849, 预测数据128208, 本次预测偏差%0.2800  
NOTICE:  样本数量392, 截距4342.9938, 斜率1.0018, 相关性0.9702  
NOTICE:  真实数据127715, 预测数据129117, 本次预测偏差%1.1000  
NOTICE:  样本数量393, 截距-32076.9878, 斜率1.3312, 相关性0.9964  
NOTICE:  真实数据124554, 预测数据124206, 本次预测偏差%0.2800  
NOTICE:  样本数量393, 截距-19541.0766, 斜率1.2152, 相关性1.0000  
NOTICE:  真实数据117397, 预测数据117404, 本次预测偏差%0.0100  
NOTICE:  样本数量390, 截距47549.0400, 斜率0.5872, 相关性0.9902  
NOTICE:  真实数据112693, 预测数据111435, 本次预测偏差%1.1200  
NOTICE:  样本数量390, 截距50098.4943, 斜率0.5560, 相关性0.9977  
NOTICE:  真实数据108804, 预测数据108821, 本次预测偏差%0.0200  
NOTICE:  样本数量390, 截距50042.2813, 斜率0.5567, 相关性0.9964  
NOTICE:  真实数据105623, 预测数据105973, 本次预测偏差%0.3300  
NOTICE:  样本数量1, 截距5273.1579, 斜率0.9358, 相关性0.8782  
NOTICE:  真实数据100474, 预测数据89115, 本次预测偏差%11.3100  
NOTICE:  样本数量1, 截距5280.4763, 斜率0.9354, 相关性0.8785  
NOTICE:  真实数据89591, 预测数据72087, 本次预测偏差%19.5400  
NOTICE:  样本数量384, 截距30325.0273, 斜率0.5354, 相关性0.9387  
NOTICE:  真实数据71422, 预测数据64918, 本次预测偏差%9.1100  
NOTICE:  样本数量386, 截距37631.4820, 斜率0.4029, 相关性0.9941  
NOTICE:  真实数据64616, 预测数据64377, 本次预测偏差%0.3700  
NOTICE:  样本数量384, 截距20707.7226, 斜率0.6191, 相关性0.9961  
NOTICE:  真实数据66389, 预测数据65428, 本次预测偏差%1.4500  
NOTICE:  样本数量384, 截距17341.5766, 斜率0.6472, 相关性0.9978  
NOTICE:  真实数据72238, 预测数据72772, 本次预测偏差%0.7400  
NOTICE:  样本数量1, 截距5202.6036, 斜率0.9363, 相关性0.8805  
NOTICE:  真实数据85644, 预测数据102774, 本次预测偏差%20.0000  
NOTICE:  样本数量382, 截距-211937.8855, 斜率2.3700, 相关性0.9232  
NOTICE:  真实数据104207, 预测数据107341, 本次预测偏差%3.0100  
NOTICE:  样本数量363, 截距10473.2297, 斜率0.9328, 相关性0.9381  
NOTICE:  真实数据134716, 预测数据144319, 本次预测偏差%7.1300  
NOTICE:  样本数量363, 截距8082.7467, 斜率0.9608, 相关性0.9426  
NOTICE:  真实数据143484, 预测数据153571, 本次预测偏差%7.0300  
NOTICE:  样本数量379, 截距90033.9242, 斜率0.4106, 相关性0.9539  
NOTICE:  真实数据151426, 预测数据150648, 本次预测偏差%0.5100  
NOTICE:  样本数量363, 截距3555.4288, 斜率1.0121, 相关性0.9344  
NOTICE:  真实数据147628, 预测数据148068, 本次预测偏差%0.3000  
NOTICE:  样本数量377, 截距-22855.0642, 斜率1.3040, 相关性0.9608  
NOTICE:  真实数据142781, 预测数据143858, 本次预测偏差%0.7500  
NOTICE:  样本数量363, 截距8135.3139, 斜率0.9564, 相关性0.9081  
NOTICE:  真实数据127852, 预测数据116232, 本次预测偏差%9.0900  
NOTICE:  样本数量363, 截距11650.2051, 斜率0.9095, 相关性0.9209  
NOTICE:  真实数据113022, 预测数据107993, 本次预测偏差%4.4500  
NOTICE:  样本数量366, 截距43850.9025, 斜率0.5911, 相关性0.9231  
NOTICE:  真实数据105932, 预测数据109352, 本次预测偏差%3.2300  
NOTICE:  样本数量366, 截距41459.4112, 斜率0.6193, 相关性0.9421  
NOTICE:  真实数据110807, 预测数据111147, 本次预测偏差%0.3100  
NOTICE:  样本数量366, 截距41099.7207, 斜率0.6234, 相关性0.9330  
NOTICE:  真实数据112531, 预测数据107192, 本次预测偏差%4.7400  
NOTICE:  样本数量366, 截距45144.8340, 斜率0.5733, 相关性0.9910  
NOTICE:  真实数据106011, 预测数据105444, 本次预测偏差%0.5400  
NOTICE:  样本数量366, 截距45652.0542, 斜率0.5670, 相关性0.9907  
NOTICE:  真实数据105170, 预测数据104365, 本次预测偏差%0.7600  
NOTICE:  样本数量368, 截距57233.9599, 斜率0.4495, 相关性0.9969  
NOTICE:  真实数据103554, 预测数据103401, 本次预测偏差%0.1500  
NOTICE:  样本数量368, 截距58816.4609, 斜率0.4327, 相关性0.9999  
NOTICE:  真实数据102706, 预测数据102719, 本次预测偏差%0.0100  
NOTICE:  样本数量366, 截距45837.1316, 斜率0.5648, 相关性0.9874  
NOTICE:  真实数据101460, 预测数据101473, 本次预测偏差%0.0100  
NOTICE:  样本数量366, 截距45788.3201, 斜率0.5655, 相关性0.9787  
NOTICE:  真实数据98505, 预测数据97660, 本次预测偏差%0.8600  
NOTICE:  样本数量1, 截距5430.0126, 斜率0.9322, 相关性0.8723  
NOTICE:  真实数据91734, 预测数据83227, 本次预测偏差%9.2700  
NOTICE:  样本数量1, 截距5423.3347, 斜率0.9320, 相关性0.8726  
NOTICE:  真实数据83453, 预测数据66847, 本次预测偏差%19.9000  
NOTICE:  样本数量360, 截距30435.2931, 斜率0.4928, 相关性0.9223  
NOTICE:  真实数据65904, 预测数据59957, 本次预测偏差%9.0200  
NOTICE:  样本数量360, 截距25313.6494, 斜率0.5394, 相关性0.9738  
NOTICE:  真实数据59911, 预测数据58046, 本次预测偏差%3.1100  
NOTICE:  样本数量360, 截距22789.5261, 斜率0.5623, 相关性0.9761  
NOTICE:  真实数据60677, 预测数据57848, 本次预测偏差%4.6600  
NOTICE:  样本数量360, 截距14289.6380, 斜率0.6383, 相关性1.0000  
NOTICE:  真实数据62350, 预测数据62309, 本次预测偏差%0.0700  
NOTICE:  样本数量1, 截距5349.6991, 斜率0.9328, 相关性0.8743  
NOTICE:  真实数据75224, 预测数据94495, 本次预测偏差%25.6200  
NOTICE:  样本数量1, 截距5276.8974, 斜率0.9345, 相关性0.8761  
NOTICE:  真实数据95563, 预测数据124211, 本次预测偏差%29.9800  
NOTICE:  样本数量339, 截距10611.8990, 斜率0.9248, 相关性0.9273  
NOTICE:  真实数据127277, 预测数据132503, 本次预测偏差%4.1100  
NOTICE:  样本数量339, 截距9346.7583, 斜率0.9398, 相关性0.9270  
NOTICE:  真实数据131802, 预测数据141158, 本次预测偏差%7.1000  
NOTICE:  样本数量354, 截距45602.8301, 斜率0.6964, 相关性0.9378  
NOTICE:  真实数据140259, 预测数据142531, 本次预测偏差%1.6200  
NOTICE:  样本数量354, 截距22118.2940, 斜率0.8984, 相关性0.9995  
NOTICE:  真实数据139179, 预测数据139044, 本次预测偏差%0.1000  
NOTICE:  样本数量339, 截距7066.6202, 斜率0.9646, 相关性0.9085  
NOTICE:  真实数据130151, 预测数据123330, 本次预测偏差%5.2400  
NOTICE:  样本数量352, 截距788258.5127, 斜率-6.1054, 相关性0.9259  
NOTICE:  真实数据120531, 预测数据120243, 本次预测偏差%0.2400  
 
     check_predict        
------------------------  
 (165320,170611,0.0320)  
 (167663,165922,0.0104)  
 (161071,150145,0.0678)  
 (145570,136026,0.0656)  
 (133155,133953,0.0060)  
 (133962,134241,0.0021)  
 (130484,127596,0.0221)  
 (126182,123864,0.0184)  
 (122998,124578,0.0128)  
 (125052,125119,0.0005)  
 (123000,121572,0.0116)  
 (119991,118710,0.0107)  
 (116182,118363,0.0188)  
 (116887,116082,0.0069)  
 (108562,98517,0.0925)  
 (99168,82725,0.1658)  
 (82505,74942,0.0917)  
 (73450,72804,0.0088)  
 (75681,76143,0.0061)  
 (82509,82187,0.0039)  
 (92670,111447,0.2026)  
 (112865,145539,0.2895)  
 (148731,150848,0.0142)  
 (149961,156169,0.0414)  
 (155748,161289,0.0356)  
 (160430,155939,0.0280)  
 (153344,150240,0.0202)  
 (147997,140772,0.0488)  
 (138023,137013,0.0073)  
 (136535,135075,0.0107)  
 (133978,133909,0.0005)  
 (132634,136891,0.0321)  
 (136998,137674,0.0049)  
 (136303,136431,0.0009)  
 (130987,130817,0.0013)  
 (127722,129731,0.0157)  
 (126303,124949,0.0107)  
 (117218,117405,0.0016)  
 (109160,110726,0.0143)  
 (96823,97097,0.0028)  
 (79716,72776,0.0871)  
 (72658,69530,0.0431)  
 (71739,71377,0.0051)  
 (77243,76786,0.0059)  
 (89412,109386,0.2234)  
 (110972,112269,0.0117)  
 (144014,149237,0.0363)  
 (148483,151688,0.0216)  
 (150405,156324,0.0394)  
 (154850,155607,0.0049)  
 (151244,144638,0.0437)  
 (141118,129415,0.0829)  
 (126106,125617,0.0039)  
 (124896,128489,0.0288)  
 (129061,128477,0.0045)  
 (127849,128208,0.0028)  
 (127715,129117,0.0110)  
 (124554,124206,0.0028)  
 (117397,117404,0.0001)  
 (112693,111435,0.0112)  
 (108804,108821,0.0002)  
 (105623,105973,0.0033)  
 (100474,89115,0.1131)  
 (89591,72087,0.1954)  
 (71422,64918,0.0911)  
 (64616,64377,0.0037)  
 (66389,65428,0.0145)  
 (72238,72772,0.0074)  
 (85644,102774,0.2000)  
 (104207,107341,0.0301)  
 (134716,144319,0.0713)  
 (143484,153571,0.0703)  
 (151426,150648,0.0051)  
 (147628,148068,0.0030)  
 (142781,143858,0.0075)  
 (127852,116232,0.0909)  
 (113022,107993,0.0445)  
 (105932,109352,0.0323)  
 (110807,111147,0.0031)  
 (112531,107192,0.0474)  
 (106011,105444,0.0054)  
 (105170,104365,0.0076)  
 (103554,103401,0.0015)  
 (102706,102719,0.0001)  
 (101460,101473,0.0001)  
 (98505,97660,0.0086)  
 (91734,83227,0.0927)  
 (83453,66847,0.1990)  
 (65904,59957,0.0902)  
 (59911,58046,0.0311)  
 (60677,57848,0.0466)  
 (62350,62309,0.0007)  
 (75224,94495,0.2562)  
 (95563,124211,0.2998)  
 (127277,132503,0.0411)  
 (131802,141158,0.0710)  
 (140259,142531,0.0162)  
 (139179,139044,0.0010)  
 (130151,123330,0.0524)  
 (120531,120243,0.0024)  
(100 rows)

Prediction curve:

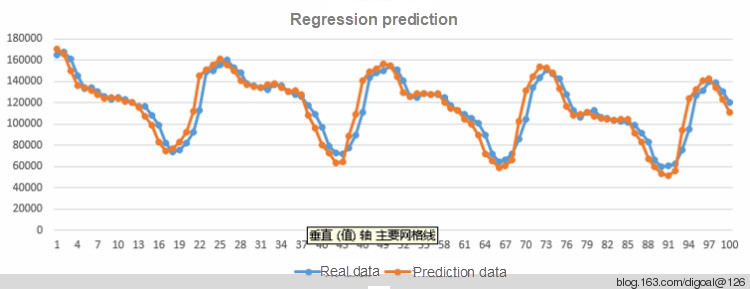
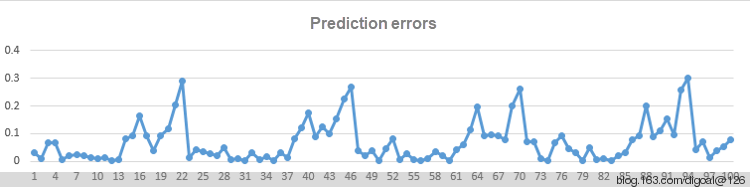
Prediction error:

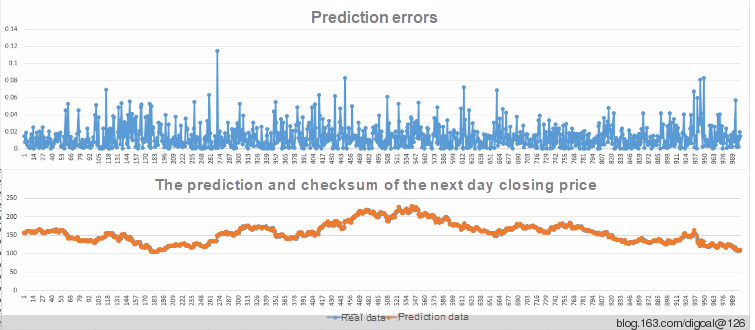
Based on simple linear regression analysis to analyze Moutai's daily closing price, the following is the next day’s closing price prediction and checksum chart.