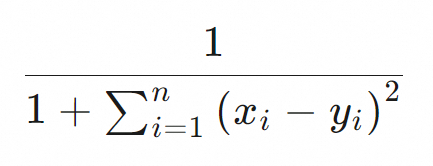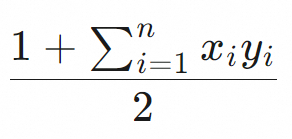如何最佳化Table Store的向量檢索效果 - Tablestore

Tablestore基於多元索引提供了向量檢索的能力，可以在大規模資料集中找到最相似的資料項目。如果您在使用向量檢索進行語義搜尋時的檢索效果不符合預期，請按照本文的排查思路進行向量檢索最佳化。

向量檢索評分公式

說明

Tablestore向量檢索（KnnVectorQuery）使用數值向量進行近似最近鄰查詢，適用於檢索增強產生（RAG）、推薦系統、相似性檢測、自然語言處理與語義搜尋等情境。如何使用向量檢索，請參見向量檢索。

向量檢索支援的距離度量演算法包括歐氏距離（euclidean）、餘弦相似性（cosine）、點積（dot_product）。不同距離度量演算法的評分公式不同，Table Store內部通過距離度量演算法的評分公式來評估向量之間的相似性。具體評分公式請參見下表。

MetricType	評分公式
歐氏距離（euclidean）
點積（dot_product）
餘弦相似性（cosine）

排查分析

1. 檢查排序方式

在使用向量檢索時，請您手動設定定序為按照分數排序，即使用ScoreSort。預設情況下按照主鍵排序。

2. 調整與BoolQuery的組合使用方式

如果您在組合使用KnnVectorQuery（向量檢索）與BoolQuery（多條件組合查詢），建議將多元索引的查詢類型設定為KnnVectorQuery。BoolQuery的查詢條件設定到Filter（向量檢索過濾器）中，不影響評分分數計算。

重要

如果您將查詢類型設定為BoolQuery，KnnVectorQuery作為BoolQuery中的子條件，則BoolQuery中的其他查詢條件可能影響評分分數的計算。更多資訊，請參見與BoolQuery組合使用說明。

以下為向量檢索的Java範例程式碼。

private static void knnVectorQuery(SyncClient client) {
    SearchQuery searchQuery = new SearchQuery();
    KnnVectorQuery query = new KnnVectorQuery();
    query.setFieldName("Col_Vector");
    query.setTopK(10); // 返回最鄰近的topK。
    query.setFloat32QueryVector(new float[]{0.1f, 0.2f, 0.3f, 0.4f});
    // 最鄰近的向量需要滿足Col_Keyword=hangzhou && Col_Long<4條件。
    query.setFilter(QueryBuilders.bool()
            .must(QueryBuilders.term("Col_Keyword", "hangzhou"))
            .must(QueryBuilders.range("Col_Long").lessThan(4))
    );
    searchQuery.setQuery(query);
    searchQuery.setLimit(10);
    // 按照分數排序。
    searchQuery.setSort(new Sort(Collections.singletonList(new ScoreSort())));
    SearchRequest searchRequest = new SearchRequest("<TABLE_NAME>", "<SEARCH_INDEX_NAME>", searchQuery);
    SearchRequest.ColumnsToGet columnsToGet = new SearchRequest.ColumnsToGet();
    columnsToGet.setColumns(Arrays.asList("Col_Keyword", "Col_Long"));
    searchRequest.setColumnsToGet(columnsToGet);
    // 訪問Search介面。
    SearchResponse resp = client.search(searchRequest);
    for (SearchHit hit : resp.getSearchHits()) {
        // 列印分數。
        System.out.println(hit.getScore());
        // 列印資料。
        System.out.println(hit.getRow());
    }
}

3. 檢查向量的產生效果

Tablestore僅對向量資料進行相似性的計算，並不涉及向量產生的效果是否最佳的問題。資料庫中的向量和查詢的向量均由外部Embedding模型產生寫入，因此在針對一些專業性特彆強的情境，產生的向量可能效果不佳。接下來針對此問題進行排查。

使用外圍（不使用Table Store）直接計算分數。
1. 將查詢的向量命名為向量a，將希望召回的Table Store表中的向量命名為向量b。
  說明
  您可以通過多元索引、二級索引或寬表資料讀取介面擷取向量b資料。
2. 根據附錄：向量檢索評分公式的示範代碼的MetricFunction.COSINE.compare(a, b)方法，計算出分數a。
使用Table Store計算分數。
使用Tablestore的向量檢索功能查詢向量a，然後查看返回結果中每行資料的分數b。
對比分析。
如果Tablestore的向量檢索中未查詢到向量b所在的行資料，則理論上返回結果中每行資料的分數b均高於分數a。
此時可驗證，Embedding模型產生效果不佳導致向量檢索效果不理想。由於在召回結果中僅存在高於使用者實際期望分數的向量資料，因此無法返回使用者所期望的較低分數的向量資料。
建議方案。
該問題一般發生在專業情境下，例如生物醫學中特殊的名詞在通用的Embedding模型下表現不佳，在專業情境下語義相近但是在模型中語義不相近，此時候您可考慮以下方案：
- 尋找專業領域的Embedding模型。
  魔搭社區提供了大量現成的Embedding模型。您可以選擇政務、電商、醫學、法律、金融等專業領域的模型。更多資訊，請參見Embedding模型列表。
- 通過合法途徑收集大量的專業語料，以此訓練一個合適的Embedding模型。

附錄：向量檢索評分公式的示範代碼

以下通過Java代碼示範距離度量演算法的評分公式。

import java.util.concurrent.ThreadLocalRandom;

public class CompareVector {

    public static void main(String[] args) {
        // a 是查詢的向量
        float[] a = randomVector(512);
        // b 是索引中期望返回的那一行向量
        float[] b = randomVector(512);
        // 這裡選擇自己多元索引中自己設定的相似性量演算法，輸出評分
        System.out.println(MetricFunction.COSINE.compare(a, b));
    }

    public static float[] randomVector(int dim) {
        float[] vec = new float[dim];
        for (int i = 0; i < dim; i++) {
            vec[i] = ThreadLocalRandom.current().nextFloat();
            if (ThreadLocalRandom.current().nextBoolean()) {
                vec[i] = -vec[i];
            }
        }
        return l2normalize(vec, true);
    }

    public static float[] l2normalize(float[] v, boolean throwOnZero) {
        double squareSum = 0.0f;
        int dim = v.length;
        for (float x : v) {
            squareSum += x * x;
        }
        if (squareSum == 0) {
            if (throwOnZero) {
                throw new IllegalArgumentException("normalize a zero-length vector");
            } else {
                return v;
            }
        }
        double length = Math.sqrt(squareSum);
        for (int i = 0; i < dim; i++) {
            v[i] /= length;
        }
        return v;
    }

    public enum MetricFunction {
        /**
         * Euclidean distance.
         */
        EUCLIDEAN {
            @Override
            public float compare(float[] v1, float[] v2) {
                return 1 / (1 + VectorUtil.squareDistance(v1, v2));
            }
        },

        /**
         * Dot product.
         */
        DOT_PRODUCT {
            @Override
            public float compare(float[] v1, float[] v2) {
                return (1 + VectorUtil.dotProduct(v1, v2)) / 2;
            }
        },

        /**
         * Cosine.
         */
        COSINE {
            @Override
            public float compare(float[] v1, float[] v2) {
                return (1 + VectorUtil.cosine(v1, v2)) / 2;
            }
        };

        public abstract float compare(float[] v1, float[] v2);
    }


    static final class VectorUtil {

        private static void checkParam(float[] a, float[] b) {
            if (a.length != b.length) {
                throw new IllegalArgumentException("vector dimensions differ: " + a.length + "!=" + b.length);
            }
        }

        public static float dotProduct(float[] a, float[] b) {
            checkParam(a, b);
            float res = 0f;
            for (int i = 0; i < a.length; i++) {
                res += b[i] * a[i];
            }
            return res;
        }

        public static float cosine(float[] a, float[] b) {
            checkParam(a, b);
            float sum = 0.0f;
            float norm1 = 0.0f;
            float norm2 = 0.0f;
            for (int i = 0; i < a.length; i++) {
                float elem1 = a[i];
                float elem2 = b[i];
                sum += elem1 * elem2;
                norm1 += elem1 * elem1;
                norm2 += elem2 * elem2;
            }
            return (float) (sum / Math.sqrt((double) norm1 * (double) norm2));
        }

        public static float squareDistance(float[] a, float[] b) {
            checkParam(a, b);
            float sum = 0.0f;
            for (int i = 0; i < a.length; i++) {
                float difference = a[i] - b[i];
                sum += difference * difference;
            }
            return sum;
        }
    }
}