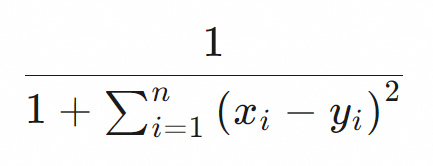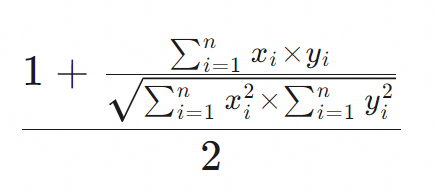如何优化表格存储的向量检索效果 - 表格存储

表格存储基于多元索引提供了向量检索的能力，可以在大规模数据集中找到最相似的数据项。如果您在使用向量检索进行语义搜索时的检索效果不符合预期，请按照本文的排查思路进行向量检索优化。

向量检索评分公式

说明

表格存储向量检索（KnnVectorQuery）使用数值向量进行近似最近邻查询，适用于检索增强生成（RAG）、推荐系统、相似性检测、自然语言处理与语义搜索等场景。如何使用向量检索，请参见向量检索介绍与使用。

向量检索支持的距离度量算法包括欧氏距离（euclidean）、余弦相似度（cosine）、点积（dot_product）。不同距离度量算法的评分公式不同，表格存储内部通过距离度量算法的评分公式来评估向量之间的相似度。具体评分公式请参见下表。

MetricType	评分公式
欧氏距离（euclidean）
点积（dot_product）
余弦相似度（cosine）

排查分析

1. 检查排序方式

在使用向量检索时，请您手动设置排序规则为按照分数排序，即使用ScoreSort。默认情况下按照主键排序。

2. 调整与BoolQuery的组合使用方式

如果您在组合使用KnnVectorQuery（向量检索）与BoolQuery（多条件组合查询），建议将多元索引的查询类型设置为KnnVectorQuery。BoolQuery的查询条件设置到Filter（向量检索过滤器）中，不影响评分分数计算。

重要

如果您将查询类型设置为BoolQuery，KnnVectorQuery作为BoolQuery中的子条件，则BoolQuery中的其他查询条件可能影响评分分数的计算。更多信息，请参见与BoolQuery组合使用说明。

以下为向量检索的Java示例代码。

private static void knnVectorQuery(SyncClient client) {
    SearchQuery searchQuery = new SearchQuery();
    KnnVectorQuery query = new KnnVectorQuery();
    query.setFieldName("Col_Vector");
    query.setTopK(10); // 返回最邻近的topK。
    query.setFloat32QueryVector(new float[]{0.1f, 0.2f, 0.3f, 0.4f});
    // 最邻近的向量需要满足Col_Keyword=hangzhou && Col_Long<4条件。
    query.setFilter(QueryBuilders.bool()
            .must(QueryBuilders.term("Col_Keyword", "hangzhou"))
            .must(QueryBuilders.range("Col_Long").lessThan(4))
    );
    searchQuery.setQuery(query);
    searchQuery.setLimit(10);
    // 按照分数排序。
    searchQuery.setSort(new Sort(Collections.singletonList(new ScoreSort())));
    SearchRequest searchRequest = new SearchRequest("<TABLE_NAME>", "<SEARCH_INDEX_NAME>", searchQuery);
    SearchRequest.ColumnsToGet columnsToGet = new SearchRequest.ColumnsToGet();
    columnsToGet.setColumns(Arrays.asList("Col_Keyword", "Col_Long"));
    searchRequest.setColumnsToGet(columnsToGet);
    // 访问Search接口。
    SearchResponse resp = client.search(searchRequest);
    for (SearchHit hit : resp.getSearchHits()) {
        // 打印分数。
        System.out.println(hit.getScore());
        // 打印数据。
        System.out.println(hit.getRow());
    }
}

3. 检查向量的生成效果

表格存储仅对向量数据进行相似度的计算，并不涉及向量生成的效果是否最佳的问题。数据库中的向量和查询的向量均由外部Embedding模型生成写入，因此在针对一些专业性特别强的场景，生成的向量可能效果不佳。接下来针对此问题进行排查。

使用外围（不使用表格存储）直接计算分数。
1. 将查询的向量命名为向量a，将希望召回的表格存储表中的向量命名为向量b。
  说明
  您可以通过多元索引、二级索引或宽表数据读取接口获取向量b数据。
2. 根据附录：向量检索评分公式的演示代码的MetricFunction.COSINE.compare(a, b)方法，计算出分数a。
使用表格存储计算分数。
使用表格存储的向量检索功能查询向量a，然后查看返回结果中每行数据的分数b。
对比分析。
如果表格存储的向量检索中未查询到向量b所在的行数据，则理论上返回结果中每行数据的分数b均高于分数a。
此时可验证，Embedding模型生成效果不佳导致向量检索效果不理想。由于在召回结果中仅存在高于用户实际期望分数的向量数据，因此无法返回用户所期望的较低分数的向量数据。
建议方案。
该问题一般发生在专业场景下，例如生物医疗中特殊的名词在通用的Embedding模型下表现不佳，在专业场景下语义相近但是在模型中语义不相近，此时候您可考虑以下方案：
- 寻找专业领域的Embedding模型。
  魔搭社区提供了大量现成的Embedding模型。您可以选择政务、电商、医疗、法律、金融等专业领域的模型。更多信息，请参见Embedding模型列表。
- 通过合法途径收集大量的专业语料，以此训练一个合适的Embedding模型。

附录：向量检索评分公式的演示代码

以下通过Java代码演示距离度量算法的评分公式。

import java.util.concurrent.ThreadLocalRandom;

public class CompareVector {

    public static void main(String[] args) {
        // a 是查询的向量
        float[] a = randomVector(512);
        // b 是索引中期望返回的那一行向量
        float[] b = randomVector(512);
        // 这里选择自己多元索引中自己设置的相似度量算法，输出评分
        System.out.println(MetricFunction.COSINE.compare(a, b));
    }

    public static float[] randomVector(int dim) {
        float[] vec = new float[dim];
        for (int i = 0; i < dim; i++) {
            vec[i] = ThreadLocalRandom.current().nextFloat();
            if (ThreadLocalRandom.current().nextBoolean()) {
                vec[i] = -vec[i];
            }
        }
        return l2normalize(vec, true);
    }

    public static float[] l2normalize(float[] v, boolean throwOnZero) {
        double squareSum = 0.0f;
        int dim = v.length;
        for (float x : v) {
            squareSum += x * x;
        }
        if (squareSum == 0) {
            if (throwOnZero) {
                throw new IllegalArgumentException("normalize a zero-length vector");
            } else {
                return v;
            }
        }
        double length = Math.sqrt(squareSum);
        for (int i = 0; i < dim; i++) {
            v[i] /= length;
        }
        return v;
    }

    public enum MetricFunction {
        /**
         * Euclidean distance.
         */
        EUCLIDEAN {
            @Override
            public float compare(float[] v1, float[] v2) {
                return 1 / (1 + VectorUtil.squareDistance(v1, v2));
            }
        },

        /**
         * Dot product.
         */
        DOT_PRODUCT {
            @Override
            public float compare(float[] v1, float[] v2) {
                return (1 + VectorUtil.dotProduct(v1, v2)) / 2;
            }
        },

        /**
         * Cosine.
         */
        COSINE {
            @Override
            public float compare(float[] v1, float[] v2) {
                return (1 + VectorUtil.cosine(v1, v2)) / 2;
            }
        };

        public abstract float compare(float[] v1, float[] v2);
    }


    static final class VectorUtil {

        private static void checkParam(float[] a, float[] b) {
            if (a.length != b.length) {
                throw new IllegalArgumentException("vector dimensions differ: " + a.length + "!=" + b.length);
            }
        }

        public static float dotProduct(float[] a, float[] b) {
            checkParam(a, b);
            float res = 0f;
            for (int i = 0; i < a.length; i++) {
                res += b[i] * a[i];
            }
            return res;
        }

        public static float cosine(float[] a, float[] b) {
            checkParam(a, b);
            float sum = 0.0f;
            float norm1 = 0.0f;
            float norm2 = 0.0f;
            for (int i = 0; i < a.length; i++) {
                float elem1 = a[i];
                float elem2 = b[i];
                sum += elem1 * elem2;
                norm1 += elem1 * elem1;
                norm2 += elem2 * elem2;
            }
            return (float) (sum / Math.sqrt((double) norm1 * (double) norm2));
        }

        public static float squareDistance(float[] a, float[] b) {
            checkParam(a, b);
            float sum = 0.0f;
            for (int i = 0; i < a.length; i++) {
                float difference = a[i] - b[i];
                sum += difference * difference;
            }
            return sum;
        }
    }
}