動機
推薦系統選擇商品展現給使用者,並期待使用者的正向反饋(點擊、成交)。然而推薦系統並不能提前知道使用者在觀察到商品之後如何反饋,也就是不能提前獲得本次推薦的收益,唯一能做的就是不停地嘗試,並即時收集反饋以便更新自己試錯的策略。目的是使得整個過程損失的收益最小。這一過程就類似與一個賭徒在賭場裡玩老虎機賭博。賭徒要去搖老虎機,走進賭場一看,一排老虎機,外表一模一樣,但是每個老虎機吐錢的機率可不一樣,他不知道每個老虎機吐錢的機率分布是什麼,那麼每次該選擇哪個老虎機可以做到最大化收益呢?這就是多臂賭博機問題(Multi-armed bandit problem, MAB)。
MAB問題的痛點是Exploitation-Exploration(E&E)兩難的問題:對已知的吐錢機率比較高的老虎機,應該更多的去嘗試(exploitation),以便獲得一定的累計收益;對未知的或嘗試次數較少的老虎機,還要分配一定的嘗試機會(exploration),以免錯失收益更高的選擇,但同時較多的探索也意味著較高的風險(機會成本)。
冷啟動問題
新上架的物品沒有歷史行為資料,如何分配流量以使使用者滿意度最大?
推薦系統中的資料迴圈問題
演算法決定展示內容,展示內容影響使用者行為,而使用者行為反饋又會決定後續演算法的學習,形成迴圈。在這種迴圈下,訓練集和測試集與監督學習獨立同分布的假設相去甚遠,同時系統層面上缺乏有效探索機制的設計,可能導致模型更聚焦於局部最優。
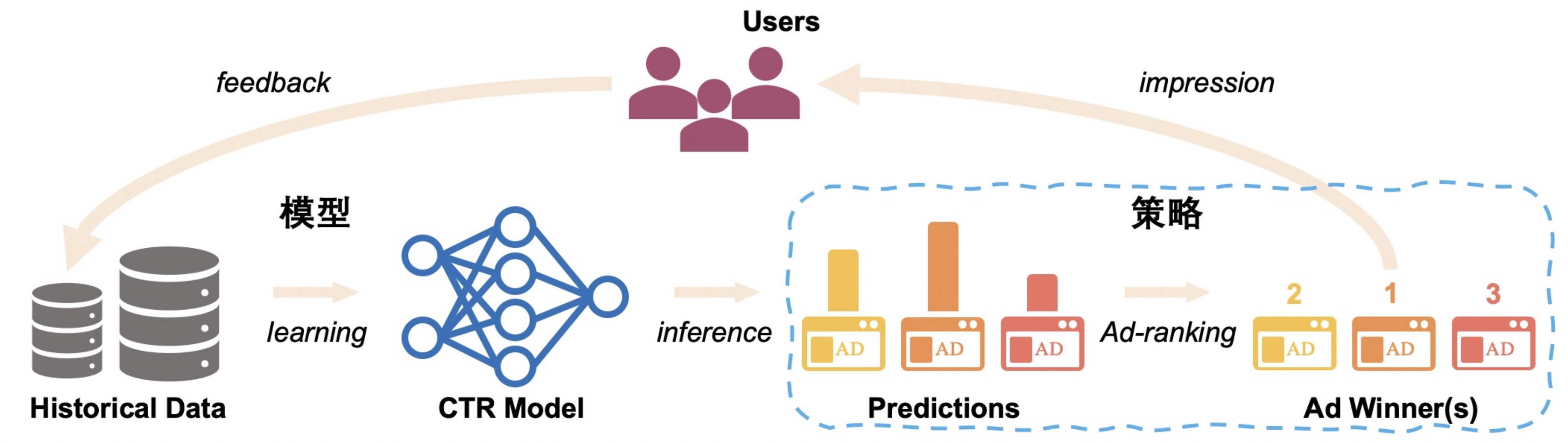
在使用者行為稀疏的情境下,資料迴圈問題尤其顯著。問題的本質:有限的資料無法獲得絕對置信的預估,探索和利用(Explore&Exploit)是突破資料迴圈的關鍵。
演算法概要描述
Bandit 演算法能較好地平衡探索和利用問題 ( E&E 問題 ),無須事先積累大量資料就能較好地處理冷啟動問題,避免根據直接收益/展現實現權重計算而產生的馬太效應,避免多數長尾、新品資源沒有任何展示機會。利用 Bandit 演算法設計的推薦演算法可以較好地解決上述問題。
根據是否考慮上下文特徵,Bandit演算法分為context-free bandit和contextual bandit兩大類。
演算法虛擬碼(single-play bandit algorithm):

與傳統方法的區別:
每個候選商品學習一個獨立的模型,避免傳統大一統模型的樣本分布不平衡問題
傳統方法採用貪心策略,盡最大可能利用已學到的知識,易因馬太效應陷入資訊繭房;Bandit演算法有顯式的exploration機制,曝光少的物品會獲得更高的展現加權
是一種線上學習方案,模型即時更新;相較A/B測試方案,能更快地收斂到最優策略
如何在一次請求中推薦多個候選物品,使用如下Multiple-Play Bandit Algorithm:
演算法詳細描述
Bandit演算法是一類用來實現Exploitation-Exploration機制的策略。根據是否考慮上下文特徵,Bandit演算法分為context-free bandit和contextual bandit兩大類。
1. UCB
Context-free Bandit演算法有很多種,比如-greedy、softmax、Thompson Sampling、UCB(Upper Confidence Bound)等。

UCB(Upper Confidence Bound - 置信上限)就是以收益(bonus)均值的信賴區間上限代表對該arm未來收益的預估值:
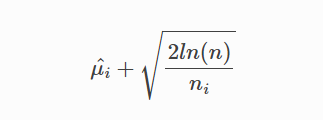

UCB在此時的決策是選擇信賴區間上界最大的arm。這個策略的好處是,能讓沒有機會嘗試的arm得到更多嘗試的機會,是騾子是馬拉出來遛遛!
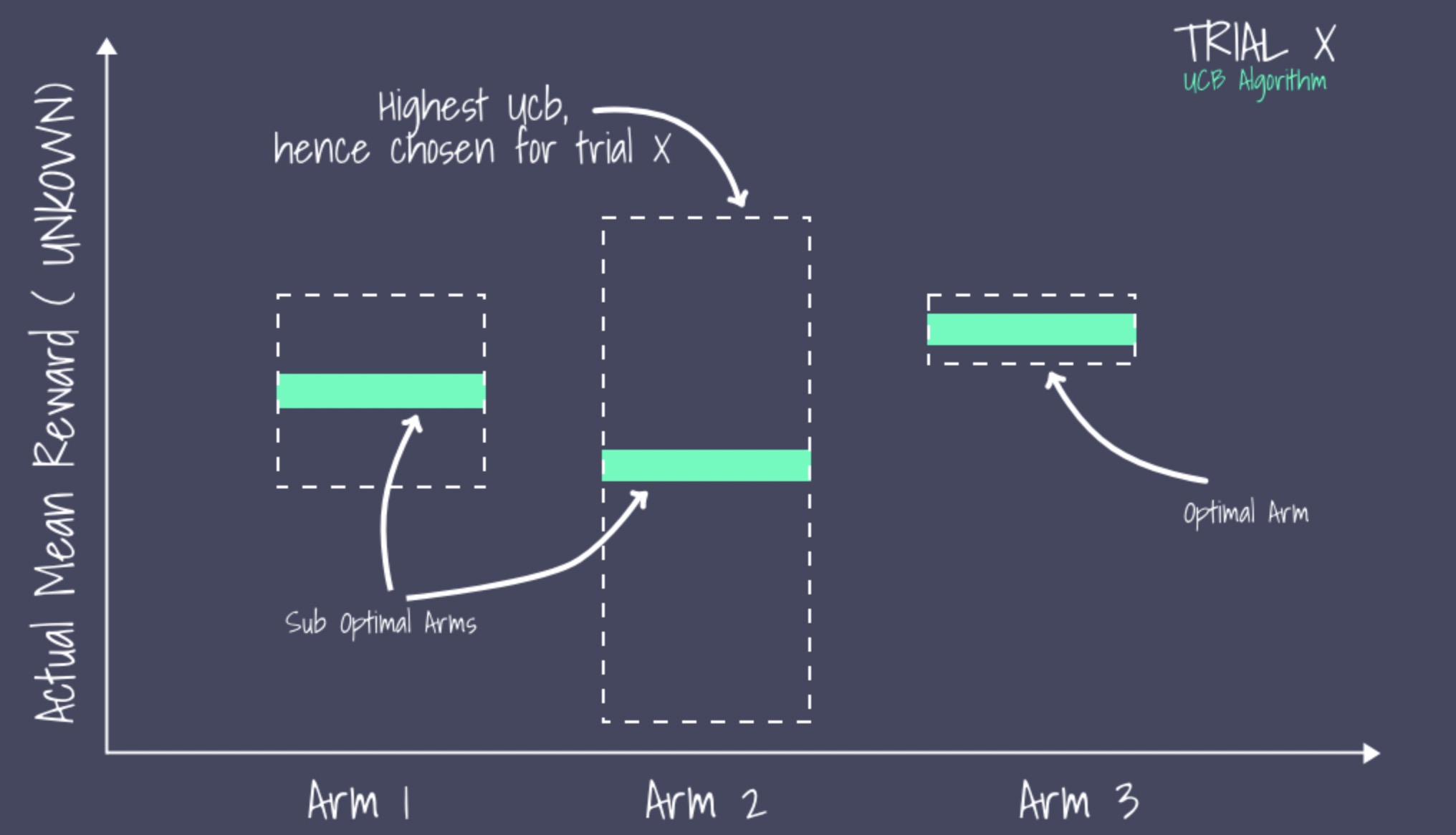
圖片和部分內容來源於在生產環境的推薦系統中部署Contextual bandit (LinUCB)演算法的經驗和陷阱 - 知乎 (zhihu.com)
對於未知或較少嘗試的arm,儘管其均值可能很低,但是由於其不確定性會導致信賴區間的上界較大,從而有較大的機率觸發exploration
對於已經很熟悉的arm(嘗試過較多次),更多的是觸發exploitation機制:如果其均值很高,會獲得更多的利用機會;反之,則會減少對其嘗試的機會
2. LinUCB
在推薦系統中,通常把待推薦的商品作為MAB問題的arm。UCB這樣的context-free類演算法,沒有充分利用推薦情境的上下文資訊,為所有使用者的選擇展現商品的策略都是相同的,忽略了使用者作為一個個活生生的個體本身的興趣點、偏好、購買力等因素都是不同的,因而,同一個商品在不同的使用者、不同的情景下接受程度是不同的。故在實際的推薦系統中,context-free的MAB演算法基本都不會被採用。
與context-free MAB演算法對應的是Contextual Bandit演算法,顧名思義,這類演算法在實現E&E時考慮了上下文資訊,因而更加適合實際的個人化推薦情境。

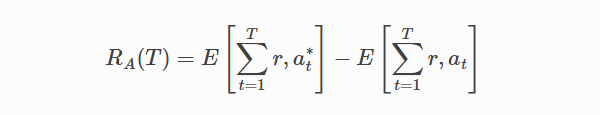
其中,T 為實驗的總步數;at* 為在時間步時有最大期望收益的arm,不能提前得知。




LinUCB演算法的優勢:
計算複雜度與arm的數量成線性關係
支援動態變化的候選arm集合
參考資料
Contextual Bandit演算法在推薦系統中的實現及應用
在生產環境的推薦系統中部署Contextual bandit演算法的經驗和陷阱
Using Multi-armed Bandit to Solve Cold-start Problems in Recommender Systems at Telco
A Multiple-Play Bandit Algorithm Applied to Recommender Systems
Adapting multi-armed bandits polices to contextual bandits scenarios