This topic describes the terms that you must understand before you use Tracing Analysis. This topic helps you understand the purpose of a distributed tracing system, what a trace is, the OpenTracing data model on which Tracing Analysis depends, and how data is reported to Tracing Analysis.
Why is a distributed tracing system needed?
To cope with various complex business requirements, developers adopt development methods such as agile development and continuous integration. The system architecture has evolved from standalone large-scale software to a microservice-based architecture. Microservices are built on different software sets. These software sets may be developed by different teams, implemented in different programming languages, or released on multiple servers. Therefore, if an error occurs in a service, dozens of applications may encounter service exceptions.
A distributed tracing system can record request information, such as the execution process and time consumption of a remote method call. A distributed tracing system is an important tool for troubleshooting system issues and system performance.
What is a trace?
Generally, a trace represents the execution process of a transaction or process in a distributed system. In the OpenTracing standard, a trace is a directed acyclic graph (DAG) that consists of multiple spans. Each span represents a named and timed segment that is continuously run in the trace.
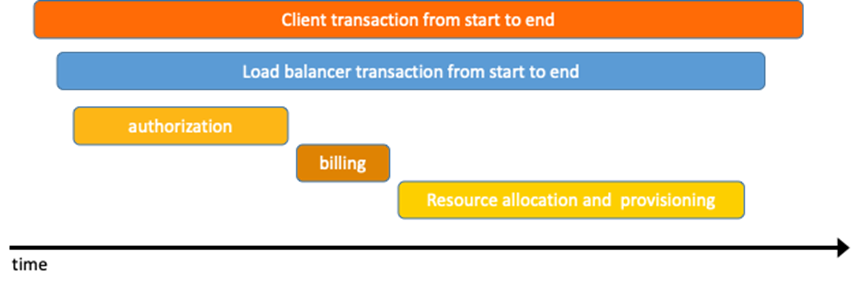
The following figure shows an example of a distributed call. When the client initiates a request, the request is first sent to the load balancer. The request is processed by the authentication service and billing service. Then, the request is sent to the requested resources. Finally, the system returns a result.

After a distributed tracing system collects and stores data, the system typically uses a sequence diagram that contains a timeline to display a trace.
OpenTracing data model
Overview
In OpenTracing, a trace is implicitly defined by the spans that belong to the trace. A trace can be considered as a DAG that consists of multiple spans. The relationships among spans are called references. The trace in the following example consists of eight spans.
Causal relationships among spans in a single trace
[Span A] ←←←(The root span)
|
+------+------+
| |
[Span B] [Span C] ←←←(ChildOf: Span C is a child node of Span A.)
| |
[Span D] +---+-------+
| |
[Span E] [Span F] >>> [Span G] >>> [Span H]
↑
↑
↑
(FollowsFrom: Span G is called after Span F.)Sometimes, a sequence diagram that contains a timeline can better display a trace.
Time relationships among spans in a single trace
––|–––––––|–––––––|–––––––|–––––––|–––––––|–––––––|–––––––|–> time
[Span A···················································]
[Span B··············································]
[Span D··········································]
[Span C········································]
[Span E·······] [Span F··] [Span G··] [Span H··]Trace
The Tracer interface provides the startSpan method for creating a span, the Extract method for extracting the context, and the Inject method for injecting the context. The Tracer interface provides the following capabilities:
Create a span or set the properties of a span.
/** Create and start a span. Then, return the span. The span contains the operation name and specified options. ** Examples: ** Create a span that does not have a parent span. ** sp := tracer.StartSpan("GetFeed") ** Create a span that has a parent span. ** sp := tracer.StartSpan("GetFeed",opentracing.ChildOf(parentSpan.Context())) **/ StartSpan(operationName string, opts ...StartSpanOption) SpanEach span contains the following objects:
- An operation name, which is also called the span name.
- A start timestamp.
- A finish timestamp.
- A collection of span tags. Each tag is a key-value pair. In the key-value pair, the key must be a string and the value can be a string, a Boolean value, or a numeric value.
- A collection of span logs. Each log consists of a key-value pair and a timestamp. In the key-value pair, the key must be a string and the value can be of any type.
- A SpanContext. Each SpanContext carries the following status data:
- Status data that identifies a span, such as the trace ID and span ID. An OpenTracing implementation depends on a distinct span to transmit the status of the current trace across process boundaries.
- Baggage items that are key-value pairs included in a trace. These key-value pairs must also be transmitted across process boundaries.
- References that indicate relationships among spans. References may include zero or multiple related spans. The spans establish the relationships based on the SpanContext.
- Inject data.
To inject data, perform the following steps:
Extract the SpanContext from a carrier.
// Inject() takes the `sm` SpanContext instance and injects it for // propagation within `carrier`. The actual type of `carrier` depends on // the value of `format`. /** Extract the SpanContext, including the trace ID, span ID, and baggage items, from a carrier based on the format parameter. ** Example: ** carrier := opentracing.HTTPHeadersCarrier(httpReq.Header) ** clientContext, err := tracer.Extract(opentracing.HTTPHeaders, carrier) **/ Extract(format interface{}, carrier interface{}) (SpanContext, error)Inject the SpanContext into a carrier.
/** ** Inject the SpanContext, including the trace ID, span ID, and baggage items, into a carrier based on the format parameter. ** Example: ** carrier := opentracing.HTTPHeadersCarrier(httpReq.Header) ** err := tracer.Inject(span.Context(), opentracing.HTTPHeaders, carrier) **/ Inject(sm SpanContext, format interface{}, carrier interface{}) error
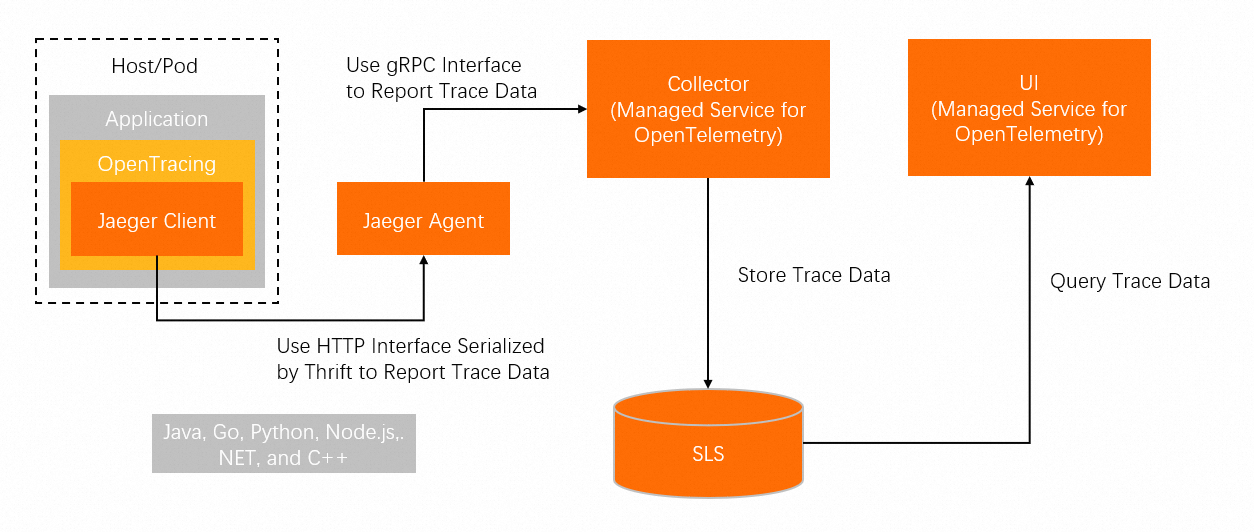
How is the data reported?
The following figure shows how data is reported without using an agent.

The following figure shows how the data is reported by using an agent.