Platform For AI:Use RNN to recognize surnames

Preparing the Data

Download the data and extract it to the current directory. Included in the data/names directory are 18 text files named as "[Language].txt". Each file contains a bunch of names, one name per line, mostly romanized (but we still need to convert from Unicode to ASCII).

from __future__ import unicode_literals, print_function, division
from io import open
import glob
import os

def findFiles(path): return glob.glob(path)

print(findFiles('data/names/*.txt'))

import unicodedata
import string

all_letters = string.ascii_letters + " .,;'"
n_letters = len(all_letters)

# Turn a Unicode string to plain ASCII, thanks to https://stackoverflow.com/a/518232/2809427
def unicodeToAscii(s):
    return ''.join(
        c for c in unicodedata.normalize('NFD', s)
        if unicodedata.category(c) != 'Mn'
        and c in all_letters
    )

print(unicodeToAscii('Ślusàrski'))

# Build the category_lines dictionary, a list of names per language
category_lines = {}
all_categories = []

# Read a file and split into lines
def readLines(filename):
    lines = open(filename, encoding='utf-8').read().strip().split('\n')
    return [unicodeToAscii(line) for line in lines]

for filename in findFiles('data/names/*.txt'):
    category = os.path.splitext(os.path.basename(filename))[0]
    all_categories.append(category)
    lines = readLines(filename)
    category_lines[category] = lines

n_categories = len(all_categories)

['data/names/Greek.txt', 'data/names/Korean.txt', 'data/names/English.txt', 'data/names/Russian.txt', 'data/names/Japanese.txt', 'data/names/German.txt', 'data/names/Scottish.txt', 'data/names/Arabic.txt', 'data/names/Czech.txt', 'data/names/Vietnamese.txt', 'data/names/Polish.txt', 'data/names/Portuguese.txt', 'data/names/Italian.txt', 'data/names/Dutch.txt', 'data/names/Irish.txt', 'data/names/Spanish.txt', 'data/names/Chinese.txt', 'data/names/French.txt']
Slusarski

print(category_lines['Italian'][:5])

['Abandonato', 'Abatangelo', 'Abatantuono', 'Abate', 'Abategiovanni']

Turning Names into Tensors

Now that we have all the names organized, we need to turn them into Tensors to make any use of them.

import torch

# Find letter index from all_letters, e.g. "a" = 0
def letterToIndex(letter):
    return all_letters.find(letter)

# Just for demonstration, turn a letter into a <1 x n_letters> Tensor
def letterToTensor(letter):
    tensor = torch.zeros(1, n_letters)
    tensor[0][letterToIndex(letter)] = 1
    return tensor

# Turn a line into a <line_length x 1 x n_letters>,
# or an array of one-hot letter vectors
def lineToTensor(line):
    tensor = torch.zeros(len(line), 1, n_letters)
    for li, letter in enumerate(line):
        tensor[li][0][letterToIndex(letter)] = 1
    return tensor

print(letterToTensor('J'))

print(lineToTensor('Jones').size())

tensor([[0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 1.,
         0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0., 0.,
         0., 0., 0.]])
torch.Size([5, 1, 57])

Creating the Network

Before autograd, creating a recurrent neural network in Torch involved cloning the parameters of a layer over several timesteps. The layers held hidden state and gradients which are now entirely handled by the graph itself. This means you can implement a RNN in a very "pure" way, as regular feed-forward layers.

import torch.nn as nn

class RNN(nn.Module):
    def __init__(self, input_size, hidden_size, output_size):
        super(RNN, self).__init__()

        self.hidden_size = hidden_size

        self.i2h = nn.Linear(input_size + hidden_size, hidden_size)
        self.i2o = nn.Linear(input_size + hidden_size, output_size)
        self.softmax = nn.LogSoftmax(dim=1)

    def forward(self, input, hidden):
        combined = torch.cat((input, hidden), 1)
        hidden = self.i2h(combined)
        output = self.i2o(combined)
        output = self.softmax(output)
        return output, hidden

    def initHidden(self):
        return torch.zeros(1, self.hidden_size)

n_hidden = 128
rnn = RNN(n_letters, n_hidden, n_categories)

input = letterToTensor('A')
hidden =torch.zeros(1, n_hidden)

output, next_hidden = rnn(input, hidden)

input = lineToTensor('Albert')
hidden = torch.zeros(1, n_hidden)

output, next_hidden = rnn(input[0], hidden)
print(output)

tensor([[-2.8313, -2.8603, -2.9229, -2.8841, -2.8769, -2.9459, -2.8800, -2.9424,
         -2.8405, -2.9202, -2.9026, -2.9292, -2.9909, -2.8454, -2.9096, -2.8061,
         -2.8472, -2.9105]], grad_fn=<LogSoftmaxBackward>)

Training

1. Preparing for Training
   Before going into training we should make a few helper functions. The first is to interpret the output of the network, which we know to be a likelihood of each category. We can use Tensor.topk to get the index of the greatest value:

   def categoryFromOutput(output):
       top_n, top_i = output.topk(1)
       category_i = top_i[0].item()
       return all_categories[category_i], category_i
   
   print(categoryFromOutput(output))

   The output is shown below.

   ('Spanish', 15)

   We will also want a quick way to get a training example (a name and its language):

   import random
   
   def randomChoice(l):
       return l[random.randint(0, len(l) - 1)]
   
   def randomTrainingExample():
       category = randomChoice(all_categories)
       line = randomChoice(category_lines[category])
       category_tensor = torch.tensor([all_categories.index(category)], dtype=torch.long)
       line_tensor = lineToTensor(line)
       return category, line, category_tensor, line_tensor
   
   for i in range(10):
       category, line, category_tensor, line_tensor = randomTrainingExample()
       print('category =', category, '/ line =', line)

   The output is shown below.

   category = Arabic / line = Fakhoury
   category = Vietnamese / line = Bui
   category = Czech / line = Buchta
   category = Arabic / line = Basara
   category = Dutch / line = Sevriens
   category = Czech / line = Cerda
   category = Russian / line = Chajengin
   category = Vietnamese / line = Vuong
   category = Russian / line = Davydov
   category = Dutch / line = Simonis

2. Training the Network

   Now all it takes to train this network is show it a bunch of examples, have it make guesses, and tell it if it's wrong.

   For the loss function nn.NLLLoss is appropriate, since the last layer of the RNN is nn.LogSoftmax.

   criterion = nn.NLLLoss()

   Each loop of training will:

   1. Create input and target tensors
   2. Create a zeroed initial hidden state
   3. Read each letter in and
   4. Keep hidden state for next letter
   5. Compare final output to target
   6. Back-propagate
   7. Return the output and loss

   learning_rate = 0.005 # If you set this too high, it might explode. If too low, it might not learn
   
   def train(category_tensor, line_tensor):
       hidden = rnn.initHidden()
   
       rnn.zero_grad()
   
       for i in range(line_tensor.size()[0]):
           output, hidden = rnn(line_tensor[i], hidden)
   
       loss = criterion(output, category_tensor)
       loss.backward()
   
       # Add parameters' gradients to their values, multiplied by learning rate
       for p in rnn.parameters():
           p.data.add_(p.grad.data, alpha=-learning_rate)
   
       return output, loss.item()

   Now we just have to run that with a bunch of examples. Since the train function returns both the output and loss we can print its guesses and also keep track of loss for plotting. Since there are 1000s of examples we print only every print_every examples, and take an average of the loss.

   import time
   import math
   
   n_iters = 100000
   print_every = 5000
   plot_every = 1000
   
   
   
   # Keep track of losses for plotting
   current_loss = 0
   all_losses = []
   
   def timeSince(since):
       now = time.time()
       s = now - since
       m = math.floor(s / 60)
       s -= m * 60
       return '%dm %ds' % (m, s)
   
   start = time.time()
   
   for iter in range(1, n_iters + 1):
       category, line, category_tensor, line_tensor = randomTrainingExample()
       output, loss = train(category_tensor, line_tensor)
       current_loss += loss
   
       # Print iter number, loss, name and guess
       if iter % print_every == 0:
           guess, guess_i = categoryFromOutput(output)
           correct = '✓' if guess == category else '✗ (%s)' % category
           print('%d %d%% (%s) %.4f %s / %s %s' % (iter, iter / n_iters * 100, timeSince(start), loss, line, guess, correct))
   
       # Add current loss avg to list of losses
       if iter % plot_every == 0:
           all_losses.append(current_loss / plot_every)
           current_loss = 0

   The output is shown below.

   5000 5% (0m 11s) 2.8952 Kinnaird / Spanish ✗ (English)
   10000 10% (0m 23s) 2.1054 Wojewodka / Russian ✗ (Polish)
   15000 15% (0m 35s) 0.7664 Rudaski / Polish ✓
   20000 20% (0m 46s) 0.9732 Yee / Chinese ✓
   25000 25% (0m 58s) 1.7527 Alesio / Portuguese ✗ (Italian)
   30000 30% (1m 10s) 0.3432 Shadid / Arabic ✓
   35000 35% (1m 22s) 0.1572 Bartalotti / Italian ✓
   40000 40% (1m 34s) 1.0907 Saliba / Arabic ✓
   45000 45% (1m 46s) 0.1409 O'Connell / Irish ✓
   50000 50% (1m 57s) 3.0025 Martell / Scottish ✗ (German)
   55000 55% (2m 9s) 2.6584 Atalian / Irish ✗ (Russian)
   60000 60% (2m 21s) 1.9061 Tasse / Japanese ✗ (French)
   65000 65% (2m 32s) 0.4886 Fernandez / Spanish ✓
   70000 70% (2m 44s) 0.4260 Acerbi / Italian ✓
   75000 75% (2m 56s) 2.0236 Longworth / Scottish ✗ (English)
   80000 80% (3m 8s) 2.4320 Oquendo / Italian ✗ (Spanish)
   85000 85% (3m 19s) 1.0514 Pesek / Czech ✓
   90000 90% (3m 31s) 1.5673 Holzer / German ✓
   95000 95% (3m 43s) 2.7059 Martin / Arabic ✗ (French)
   100000 100% (3m 55s) 2.2362 Rosenfeld / English ✗ (German)

Plotting the Results

Plotting the historical loss from all_losses shows the network learning:

import matplotlib.pyplot as plt
import matplotlib.ticker as ticker

plt.figure()
plt.plot(all_losses)

The output is shown below.

[<matplotlib.lines.Line2D at 0x7f3ce43b6e80>]

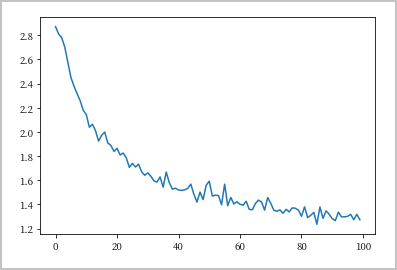
Evaluating the Results

To see how well the network performs on different categories, we will create a confusion matrix, indicating for every actual language (rows) which language the network guesses (columns). To calculate the confusion matrix a bunch of samples are run through the network with evaluate(), which is the same as train() minus the backprop.

# Keep track of correct guesses in a confusion matrix
confusion = torch.zeros(n_categories, n_categories)
n_confusion = 10000

# Just return an output given a line
def evaluate(line_tensor):
    hidden = rnn.initHidden()

    for i in range(line_tensor.size()[0]):
        output, hidden = rnn(line_tensor[i], hidden)

    return output

# Go through a bunch of examples and record which are correctly guessed
for i in range(n_confusion):
    category, line, category_tensor, line_tensor = randomTrainingExample()
    output = evaluate(line_tensor)
    guess, guess_i = categoryFromOutput(output)
    category_i = all_categories.index(category)
    confusion[category_i][guess_i] += 1

# Normalize by dividing every row by its sum
for i in range(n_categories):
    confusion[i] = confusion[i] / confusion[i].sum()

# Set up plot
fig = plt.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(confusion.numpy())
fig.colorbar(cax)

# Set up axes
ax.set_xticklabels([''] + all_categories, rotation=90)
ax.set_yticklabels([''] + all_categories)

# Force label at every tick
ax.xaxis.set_major_locator(ticker.MultipleLocator(1))
ax.yaxis.set_major_locator(ticker.MultipleLocator(1))

# sphinx_gallery_thumbnail_number = 2
plt.show()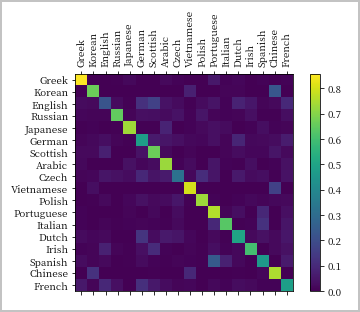

You can pick out bright spots off the main axis that show which languages it guesses incorrectly, e.g. Chinese for Korean, and Spanish for Italian. It seems to do very well with Greek, and very poorly with English (perhaps because of overlap with other languages).

Running on User Input

def predict(input_line, n_predictions=3):
    print('\n> %s' % input_line)
    with torch.no_grad():
        output = evaluate(lineToTensor(input_line))

        # Get top N categories
        topv, topi = output.topk(n_predictions, 1, True)
        predictions = []

        for i in range(n_predictions):
            value = topv[0][i].item()
            category_index = topi[0][i].item()
            print('(%.2f) %s' % (value, all_categories[category_index]))
            predictions.append([value, all_categories[category_index]])

predict('Dovesky')
predict('Jackson')
predict('Satoshi')

> Dovesky
(-0.30) Russian
(-1.76) Czech
(-3.54) English

> Jackson
(-0.07) Scottish
(-3.31) English
(-4.89) Russian

> Satoshi
(-0.84) Japanese
(-1.88) Italian
(-2.12) Arabic

predict('yuze')

> yuze
(-1.61) Japanese
(-1.64) French
(-2.11) English

• data.py (loads files)
• model.py (defines the RNN)
• train.py (runs training)

  Run train.py to train and save the network.

• predict.py (runs predict() with command line arguments)
  Run predict.py with a name to view predictions:

  $ python predict.py Hazaki
  (-0.42) Japanese
  (-1.39) Polish
  (-3.51) Czech

• server.py (serve prediction as a JSON API with bottle.py)