Libratus is an artificial intelligence computer program designed to play poker, specifically no-limit Texas hold'em. Its creators, Professor Tuomas Sandholm and his student Noam Brown from CMU intend for it to be like other, non-Poker-specific applications.
In January 2017, Libratus took on four professional poker players, beating all of them handily and winning nearly all the chips in play. Then, in November of 2017, the paper co-authored by Noam Brown and Tuomas Sandholm, "Safe and Nested Endgame Solving for Imperfect-information Games", received the NIPS 2017 Best Thesis Award.
However, the thesis did not spark particularly passionate debate among Chinese AI experts. There are three possible reasons for the lack of enthusiasm:
In November 8 2017, I had the opportunity to meet Professor Tuomas Sandholm at the AI World 2017 hosted by AI Era, where he delivered a keynote speech. Conversing over dinner, Professor Sandholm explained to me that, from the perspective of application, Libratus' algorithm does not restrict the application to only gambling. Users can use it for negotiations, auction pricing, investment decisions, and much more.

Image 1. November 8th, Tuomas Sandholm (middle) arrived at Beijing to attend AI World 2017. He is with the founder and CEO of AI Era Yang Jing (left) and the author of this article Dr. Deng Kan.
In terms of methodology, the Libratus algorithm is a combination of both Game Theory and operations research. Markov decision making process and dynamic planning comprise the theoretical foundation of reinforcement learning. Even though the sources are different, the two will eventually converge.
I believe that the collision of the Libratus algorithm with reinforcement learning and deep learning will be an amazing step forward for AI.
John Von Neumann once said, "Life is not like Go, where you can see all of the pieces on the board. Real life is full of bluffing, deception, and speculation about what is going on in the minds of others. This is the Game Theory that I study."
Understanding the Libratus paper requires you to understand four key concepts.
In the following sections, I have described these four components of Libratus thesis.
Libratus is currently only capable of playing two-person poker. However, future improvements to the algorithm and the addition of more GPUs could allow it to play against multiple opponents at the same time.
When playing Texas hold'em, each player is first dealt a hand of two cards, and then the poker dealer reveals five more cards in succession. There are four rounds of betting, after which the players compare their hands to see who wins.

Image 2. A game of Texas hold'em poker
It can be very difficult to guess the two cards in your opponent's hand. Public information includes the five community cards as well as both parties' betting history. However, your opponents will not necessarily bet strictly according to their hand. Instead, they will mix in tactics meant to deceive you.
Actually, Libratus does not speculate on its opponent's betting strategy.
To be a bit more specific, Libratus' only goal is to reach the Nash Equilibrium Strategy. Nash was a famous mathematician and the subject of the film "A Beautiful Mind." The goal of Nash Equilibrium Strategy is to avoid giving your opponent any easy wins.
Nash Equilibrium strategy is a passive defense strategy, rather than an active attack strategy. It does not attempt to speculate on the opponent's betting strategy.
For example, if the opponent's strategy is to blindly and mindlessly call your bet no matter what, Nash Equilibrium would dictate that you do not raise the stakes when our hand is good in order to take advantage of your opponent's strategy. It does this after playing a few hands in which it discovers your opponent's game plan.
But, what's stopping your opponent from finding vulnerabilities in the Nash Equilibrium Strategy? In theory, Nash Equilibrium Strategy guarantees that after playing a few hands and eliminating potential luck factors, there will be absolutely no vulnerabilities for the opponent to exploit.
The question is whether Libratus adheres strictly to Nash Equilibrium Strategy. The purpose of the mathematical proofs occupying such a large section of this paper is to prove that, at least in one on one Texas hold'em, the Libratus algorithm is a close approximation of Nash Equilibrium Strategy.
Since the Nash Equilibrium Strategy does not attempt to determine the opponent's strategy, we can use recursive machine Game Theory to analyze every possible hand combination and find the best possible betting strategy.
To determine the most optimal betting strategy, begin by creating a betting table with seven columns and several rows.
Column 1: The two cards in our hand.
Column 2: The community cards already on the table, of which there are five at most.
Column 3: Each party's betting history
Column 4: Place all the remaining chips. We can use the third column (betting history) to calculate the value in column four (our remaining chips). The fourth column is included simply for the sake of convenience.
Column 5: The two cards in our opponent's hand
Column 6: The chips we are planning to bet in the next round
Column 7: Expected profit from the strategy in column six
The first four columns are inputs, called the "situation" in the paper (Information Set, InfoSet). The last three columns are outputs, namely an estimation of hidden information, a strategy, and predicted benefit.
With enough computing power, we would be able to calculate every possible situation (InfoSet).
If we add the possible combinations in column one and column two together, we get a total of 1,326 * 43,316,000 = 57,437,316,000 combinations.
There are even more possible combinations of values in column three, betting history. This means that the table is extensively large, in fact 10165 rows in the thesis paper. This data volume is simply too vast. Even with the most powerful computer currently available, running all of the numbers would take several decades of years.
However, if we had enough computing power to traverse the table, we would be able to calculate the average profit from every betting strategy for every card combination. For example, after participants have revealed the fifth community card (the river), the opponent's hand could be one of (4544)/ (21) = 990 combinations of cards. Furthermore, the first three rounds of betting (pre-flop, flop, turn) could take any of N different forms. At this point, during our round of betting, each betting strategy, for example going all in, could yield one of 990N possible profits. The average of these 990N profit values is the average value of the betting strategy.
Faced with a certain combination of cards, we can then calculate the average profit from each possible betting strategy and select the strategy with the highest average. You must be wondering if the betting strategy with the highest average profit is the Nash Equilibrium Strategy? No, it's not.
Why? You see, if our opponent's hand is weak, for example a 3 of hearts and a 6 of clubs, then the chances of him betting a large amount are quite low.
Then how are we supposed to calculate the probability of an opponent's betting strategy?
This problem is more complicated as the opponent determines his betting strategy not only by his own cards and the community cards, but by our betting history and his estimation of our cards.
Counterfactual Best Response (CBR) is an algorithm to find the Nash Equilibrium Strategy which has recently enjoyed quite a bit of popularity.
There are three main elements to Counterfactual Best Response:
In the face of a game situation (InfoSet) or the data in the first four columns in our betting table, we start by first assuming that we take a random equal probability approach to choosing our betting strategy. We use this method as we go through a series of dealing and betting cycles, calculating our wins or losses after each round.
After a few million rounds, we will have already covered a wide range of game situations.
Subsequently, we enter the regret phase. Regretting refers to the situation where we stop using random betting and rather choose a specific strategy, for example calling the opponent's bet, in each game situation.
This phase also features a specific game situation or set value for each of the four columns in our betting table. After regretting, the next community cards to be revealed do not change. However, both our and our opponent's betting strategies change.
We then re-simulate the previous rounds. During the re-simulation, both players' hands, the cards on the table, their dealing order, and the betting prior to the regretting phase remain unchanged. However, betting after the regretting phase does change. During each betting phase, aside from the strategy specified during the regretting phase, other betting strategies remain unchanged.
Once this simulation is complete, we can calculate the average profit from the regret strategy.
Moving on, switch to another regret strategy to use under the same game situation. For example, if the prior regret phase used the call strategy, then for the next simulation we might switch to a raise strategy and re-simulate the previous game situations. This way we can calculate the average profit for the second regret strategy.
After running enough of these simulations, we can calculate the average profit for each regret strategy in different game situations. We then repeat the above process to confirm the outcomes of different strategies.
Finally, we use this data to update the betting table (Action Mapping). To use the data start by clearing the fifth column in the table, ensuring that you do not calculate the two cards in the opponent's hand. In the seventh column, enter the average profit for each betting strategy.
This was the first round of simulation and regretting. Next, we initiate the second round of simulation.
During the second round of simulation, we first assume that the opponent is still using probability of random equality to choose their betting strategy. We then select our betting strategy according to the updated betting table.
When we encounter a new game situation, or different values in the first four columns, we use the following method to select a betting strategy:
Now that we have determined the hands, dealing order, and initial betting history of the players for the second round of simulation, we can begin the regretting phase. The next step includes making another betting table recording with its corresponding betting strategy and average profit under different game situations.
In the third round of simulation, we use the second version of the betting table, while the opponent uses the first version. After several rounds of simulation, we can generate our third betting table.
The last phase is to reiterate this process over and over. After several simulation iterations, the betting table we are left with will be a close approximation of the Nash Equilibrium Strategy.
As we mentioned in the previous section, the two columns alone in the betting table contain a maximum of 57,437,016,000 different combinations of values. Adding every possible combination of betting history will result in 10165 possible value combinations
Furthermore, we must go through several billion simulations when we use Counterfactual Best Response to look for the Nash Equilibrium Strategy.
The massive amount of data in the betting table combined with the billions of simulations required by the Counterfactual Best Response method means that the entire process requires an absurd amount of computing power that would be, at best, incredibly difficult to produce.
One obvious solution would be to produce a smaller betting table by way of simplifying the game situation via abstraction.
For example, imagine you have two pairs. One pair is an 8 of hearts and an 8 of spades, the other pair is an 8 of diamonds and 8 of clubs. For the purposes of poker, these are equal in value. Therefore, we can take every combination of two 8s, (43)/ (21) = 6 combinations in total and condense them into one row in the betting table.
However, calculations of card values must be distinct. For instance, is a pair of 8s more valuable than an 8 and a 9? Presuming that the 5 community cards are revealed to be a 7, a 10, a Jack, and two irrelevant cards, then you can combine the 8 and 9 with the community cards to create a straight from 7 to Jack. While the pair of 8s is still just a pair of 8s.
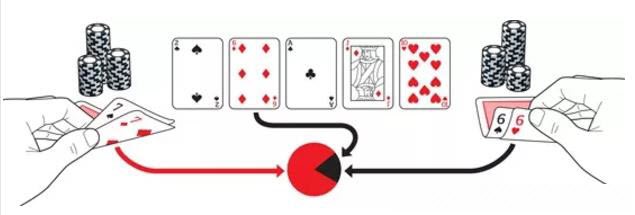
Image 3. The value of pairs is dependent on the value of the cards.
Therefore, when we calculate the value of a pair of cards, we cannot simply look at their own intrinsic value, but must also take into consideration their value in combination with the community cards once those cards are revealed.
We not only have to abstract card values, but you need to abstract bets as well. You can do this by reducing them to the four types – "fold", "call", "raise", and "all in". After going through this abstraction process, the number of data combinations in our table is greatly reduced. Once we have reduced the amount of data we need to operate on, the Counterfactual Best Response calculation becomes much more possible.
Simplifying the game situation can also lead to miscalculations. For example, we could mistakenly equate a pair of 7s to a pair of 8s. Be that as it may, if both parties keep betting and neither party folds, their cards will inevitably be shown, at which point the pair of 7s will lose to the pair of 8s, even though the difference between them is small. This is what we call an off-tree problem.
When we encounter an off-tree problem, we can solve it by replacing abstraction with resolving.
The core concept of resolving is to reverse the players' betting histories to fit data on the opponent's hand and its probability.
For instance, if you represent your hand by h1 and h2 represents your opponent's hand. Additionally, both the players are betting using Counterfactual Best Response strategy. We then can calculate the probabilities of different bets by looking up corresponding information on our betting table.
If our pre-flop hand is a pair of 8s while our opponent's hand is a pair of Aces, then the probability of us raising in the first round of betting is rather high, while the probability of winning is nearly 0. However, the probability of our opponent winning is much higher.
Now, given a specific betting history, we can use the betting table to calculate the probability of different betting strategies in the next step. The betting history is just a series of bets, while the betting history probability is the product of a series of probabilities.
By calculating betting history probabilities, we can not only estimate the cards in our opponent's hand, but we can also calculate the degree of deviation between our opponent's optimal betting strategy and his actual one. We can calculate the probability that our opponent is bluffing.
Once we have guessed our opponent's cards and the probability that he's bluffing, end game re-solving becomes quite simple. It's really nothing more than comparing our hand to our opponent's, calculating our chance at winning, and then using that data to determine how much to bet.
The introduction of an AI system like Libratus is one of many ways through which AI is changing the way we understand human intelligence. I hope this article helped you understand how Libratus functions and it could beat its competitors. I am sure with time we will witness similar programs for other games as well.
A Quick Guide to Analyzing Apache Logs on Alibaba Cloud Log Service

2,593 posts | 792 followers
FollowAlibaba Clouder - October 28, 2019
Alibaba Cloud Community - September 15, 2022
Alibaba Clouder - August 17, 2017
Apache Flink Community China - December 25, 2019
Alibaba Clouder - July 18, 2019
Alibaba Clouder - November 19, 2018

2,593 posts | 792 followers
Follow Platform For AI
Platform For AI
A platform that provides enterprise-level data modeling services based on machine learning algorithms to quickly meet your needs for data-driven operations.
Learn More AI Acceleration Solution
AI Acceleration Solution
Accelerate AI-driven business and AI model training and inference with Alibaba Cloud GPU technology
Learn More Offline Visual Intelligence Software Packages
Offline Visual Intelligence Software Packages
Offline SDKs for visual production, such as image segmentation, video segmentation, and character recognition, based on deep learning technologies developed by Alibaba Cloud.
Learn More Tongyi Qianwen (Qwen)
Tongyi Qianwen (Qwen)
Top-performance foundation models from Alibaba Cloud
Learn MoreMore Posts by Alibaba Clouder